
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的值;
的值;
(2)设![]() ,试讨论函数
,试讨论函数![]() 的单调性;
的单调性;
(3)当![]() 时,若存在正实数
时,若存在正实数![]() 满足
满足![]() ,求证:
,求证:![]() .
.
【答案】(1)1(2)见解析(3)见解析
【解析】
(1)求出函数![]() 的导数
的导数![]() ,根据
,根据![]() 求出a的值,再进行检验;
求出a的值,再进行检验;
(2)求出函数g(x)的导数,通过讨论a的范围,判断函数的单调性;;
(3)结合已知条件与对数的运算性质,得![]() .令
.令![]() ,构造函数
,构造函数![]() ,然后利用导数判断函数单调性得
,然后利用导数判断函数单调性得![]() ,进而得证
,进而得证![]() .
.
(1)因为![]() ,所以
,所以![]() ,因为
,因为![]() 在
在![]() 处取得极值,所以
处取得极值,所以![]() ,解得
,解得![]() .
.
验证:当![]() 时,
时,![]() ,易得
,易得![]() 在
在![]() 处取得极大值.
处取得极大值.
(2)因为![]() ,
,
所以![]() .
.
①若![]() ,则当
,则当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 函数
函数![]() 在
在![]() 上单调递减.
上单调递减.
②若![]() ,
,![]() ,
,
当![]() 时,易得函数
时,易得函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 恒成立,所以函数
恒成立,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,易得函数
时,易得函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(3)证明:当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() .
.
令![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
所以函数![]() 在
在![]() 时,取得最小值,最小值为
时,取得最小值,最小值为![]() . 所以
. 所以![]() ,
,
即![]() ,所以
,所以![]() 或
或![]() .
.
因为![]() 为正实数,所以
为正实数,所以![]() .
.
当![]() 时,
时,![]() ,此时不存在
,此时不存在![]() 满足条件,
满足条件,
所以![]() .
.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒1个单位的去污剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
(Ⅰ)若一次喷洒4个单位的去污剂,则去污时间可达几天?
(Ⅱ)若第一次喷洒2个单位的去污剂,6天后再喷洒![]()
![]() 个单位的去污剂,要使接下来的4天中能够持续有效去污,试求
个单位的去污剂,要使接下来的4天中能够持续有效去污,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】开发商现有四栋楼A,B,C,D.楼D位于BC间,到楼A,B,C的距离分别为![]() ,
,![]() ,
,![]() ,且从楼D看楼A,B的视角为
,且从楼D看楼A,B的视角为![]() .如图所示,不计楼大小和高度.
.如图所示,不计楼大小和高度.
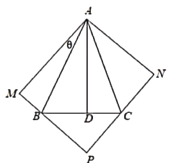
(1)试求从楼A看楼B,C视角大小;
(2)开发商为谋求更大开发区域,拟再建三栋楼M,P,N,形成以楼AMPN为顶点的矩形开发区域,规划要求楼B,C分别位于楼MP和楼PN间,如图所示,记![]() ,当
,当![]() 等于多少时,矩形开发区域面积最大?
等于多少时,矩形开发区域面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.则获得复赛资格的人数为( )
内,其频率分布直方图如图.则获得复赛资格的人数为( )
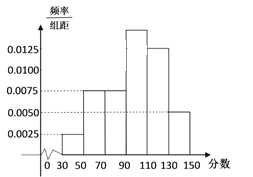
A. 520 B. 540 C. 620 D. 640
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要建造一段![]() 长的高速公路,工程队需要把380名施工人员分为两组,一组负责
长的高速公路,工程队需要把380名施工人员分为两组,一组负责![]() 的软土地带的施工,另一组完成剩下的
的软土地带的施工,另一组完成剩下的![]() 硬土地带的施工.根据工程技术人员的测算,软、硬地带每米公路的工程量分别为50人·天和30人·天.
硬土地带的施工.根据工程技术人员的测算,软、硬地带每米公路的工程量分别为50人·天和30人·天.
(1)设参与软土地带工作的人数为![]() 人,试分别写出在软、硬地带筑路的时间
人,试分别写出在软、硬地带筑路的时间![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)问如何安排两组的人数,才能使全队筑路工期最短?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的等腰梯形ABCD中,![]() ,
,![]() ,E为CD中点.若沿AE将三角形DAE折起,并连接DB,DC,得到如图所示的几何体D-ABCE,在图中解答以下问题:
,E为CD中点.若沿AE将三角形DAE折起,并连接DB,DC,得到如图所示的几何体D-ABCE,在图中解答以下问题:
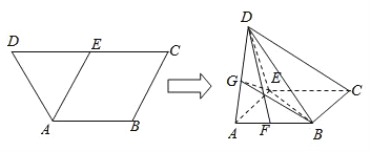
(1)设G为AD中点,求证:![]() 平面GBE;
平面GBE;
(2)若平面![]() 平面ABCE,且F为AB中点,求证:
平面ABCE,且F为AB中点,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com