
(Ⅰ)证明![]() ;
;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)比较![]() 的大小.
的大小.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
 A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:
A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:| PB |
| PA |
| 1 |
| 2 |
| PC |
| PD |
| 1 |
| 3 |
| BC |
| AD |
|
| 2 |
| cosθ-sinθ |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
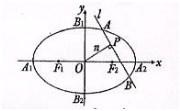 如图,椭圆C2
如图,椭圆C2| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| OP |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.
请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.| PB |
| PA |
| 1 |
| 2 |
| PC |
| PD |
| 1 |
| 3 |
| BC |
| AD |
| ||
| 6 |
| ||
| 6 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2004年湖南省高考数学试卷(理科)(解析版) 题型:解答题
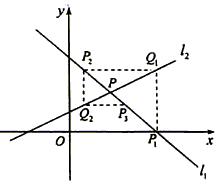
 相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1、Q1、P2、Q2,…,点Pn(n=1,2,…)的横坐标构成数列{xn}.
相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1、Q1、P2、Q2,…,点Pn(n=1,2,…)的横坐标构成数列{xn}. ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com