
ЎҫМвДҝЎҝ¶«ЭёКРДіёЯј¶ЦРС§ФЪҪсДк4ФВ·Э°ІЧ°БЛТ»ЕъҝХөчЈ¬№ШУЪХвЕъҝХөчөДК№УГДкПЮ![]() ЈЁөҘО»ЈәДкЈ¬
ЈЁөҘО»ЈәДкЈ¬ ![]() Ј©әНЛщЦ§іцөДО¬»Ө·СУГ
Ј©әНЛщЦ§іцөДО¬»Ө·СУГ![]() ЈЁөҘО»ЈәНтФӘЈ©і§јТМṩөДНіјЖЧКБПИзПВЈә
ЈЁөҘО»ЈәНтФӘЈ©і§јТМṩөДНіјЖЧКБПИзПВЈә

ЈЁ1Ј©ЗлёщҫЭТФЙПКэҫЭЈ¬УГЧоРЎ¶юіЛ·ЁФӯАнЗуіцО¬»Ө·СУГ![]() №ШУЪ
№ШУЪ![]() өДПЯРФ»Ш№й·ҪіМ
өДПЯРФ»Ш№й·ҪіМ![]() Ј»
Ј»
ЈЁ2Ј©Иф№ж¶ЁөұО¬»Ө·СУГ![]() і¬№э13.1НтФӘКұЈ¬ёГЕъҝХөчұШРлұЁ·ПЈ¬КФёщҫЭЈЁ1Ј©өДҪбВЫЗуёГЕъҝХөчК№УГДкПЮөДЧоҙуЦө.
і¬№э13.1НтФӘКұЈ¬ёГЕъҝХөчұШРлұЁ·ПЈ¬КФёщҫЭЈЁ1Ј©өДҪбВЫЗуёГЕъҝХөчК№УГДкПЮөДЧоҙуЦө.
ІОҝј№«КҪЈәЧоРЎ¶юіЛ№АјЖПЯРФ»Ш№й·ҪіМ![]() ЦРПөКэјЖЛ㹫КҪЈә
ЦРПөКэјЖЛ㹫КҪЈә
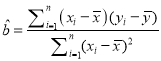 Ј¬
Ј¬ ![]()
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©ёГЕъҝХөчК№УГДкПЮөДЧоҙуЦөОӘ11ДкЎЈ
Ј»ЈЁ2Ј©ёГЕъҝХөчК№УГДкПЮөДЧоҙуЦөОӘ11ДкЎЈ
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©ПИЗуБҪЧйКэҫЭөДЖҪҫщКэЈ¬ФЩҙъИлПа№ШПөКэ№«КҪ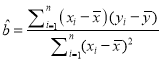 Зуіц
Зуіц![]() Ј¬Ҫш¶шИ·¶Ё
Ј¬Ҫш¶шИ·¶Ё![]() Ј¬Зуіц»Ш№й·ҪіМ
Ј¬Зуіц»Ш№й·ҪіМ![]() Ј»ЈЁ2Ј©ТАҫЭМвЙиҪЁБўІ»өИКҪ
Ј»ЈЁ2Ј©ТАҫЭМвЙиҪЁБўІ»өИКҪ![]() Ј¬Ҫвіц
Ј¬Ҫвіц![]() Ј¬ЗуіцҝХөчК№УГДкПЮөДЧоҙуЦөОӘ11ДкЈә
Ј¬ЗуіцҝХөчК№УГДкПЮөДЧоҙуЦөОӘ11ДкЈә
ҪвЈәЈЁ1Ј©ТтОӘ![]() Ј¬
Ј¬ ![]() Ј¬ЛщТФ
Ј¬ЛщТФ
![]()
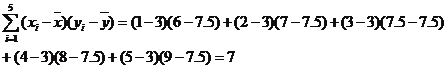
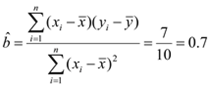
![]()
№КПЯРФ»Ш№й·ҪіМОӘ![]() .
.
ЈЁ2Ј©өұО¬»Ө·СУГ![]() і¬№э13.1НтФӘКұЈ¬јҙ
і¬№э13.1НтФӘКұЈ¬јҙ![]()
![]()
![]() ҙУөЪ12ДкҝӘКјХвЕъҝХөчұШРлұЁ·ПЈ¬ёГЕъҝХөчК№УГДкПЮөДЧоҙуЦөОӘ11Дк. ЎӯЎӯЎӯЎӯ11·Ц
ҙУөЪ12ДкҝӘКјХвЕъҝХөчұШРлұЁ·ПЈ¬ёГЕъҝХөчК№УГДкПЮөДЧоҙуЦөОӘ11Дк. ЎӯЎӯЎӯЎӯ11·Ц
ҙрЈәёГЕъҝХөчК№УГДкПЮөДЧоҙуЦөОӘ11Дк.


 ҝЪЛгМвМмМмБ·ПөБРҙр°ё
ҝЪЛгМвМмМмБ·ПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј¬
Ј¬ ![]() Ј®
Ј®
ЈЁўсЈ©өұ![]() КұЈ¬
КұЈ¬ ![]() әгіЙБўЈ¬Зу
әгіЙБўЈ¬Зу![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ЈЁўтЈ©өұ![]() КұЈ¬СРҫҝәҜКэ
КұЈ¬СРҫҝәҜКэ![]() өДБгөгёцКэЈ»
өДБгөгёцКэЈ»
ЈЁўуЈ©ЗуЦӨЈә ![]() (ІОҝјКэҫЭЈә
(ІОҝјКэҫЭЈә ![]() )Ј®
)Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() ЈЁЈ©өДҪ№ҫаОӘ4Ј¬ЧуЎўУТҪ№өг·ЦұрОӘ
ЈЁЈ©өДҪ№ҫаОӘ4Ј¬ЧуЎўУТҪ№өг·ЦұрОӘ![]() Ј¬ЗТ
Ј¬ЗТ![]() УлЕЧОпПЯ
УлЕЧОпПЯ![]() Јә
Јә ![]()
![]() өДҪ»өгЛщФЪөДЦұПЯҫӯ№э
өДҪ»өгЛщФЪөДЦұПЯҫӯ№э![]() .
.
ЈЁўсЈ©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁўтЈ©№э![]()
![]() өДЦұПЯ
өДЦұПЯ![]()
![]() Ул
Ул![]() Ҫ»УЪ
Ҫ»УЪ![]() БҪөгЈ¬УлЕЧОпПЯ
БҪөгЈ¬УлЕЧОпПЯ![]() ОЮ№«№ІөгЈ¬Зу
ОЮ№«№ІөгЈ¬Зу![]() өДГж»эөДИЎЦө·¶О§.
өДГж»эөДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙиәҜКэfЈЁxЈ©=2cos2x+ ![]() sin2x©Ғ1Ј®
sin2x©Ғ1Ј®
ЈЁ1Ј©ЗуfЈЁxЈ©өДЧоҙуЦөј°ҙЛКұөДxЦө
ЈЁ2Ј©ЗуfЈЁxЈ©өДөҘөчјхЗшјд
ЈЁ3Ј©ИфxЎК[©Ғ ![]() Ј¬
Ј¬ ![]() ]КұЈ¬ЗуfЈЁxЈ©өДЦөУтЈ®
]КұЈ¬ЗуfЈЁxЈ©өДЦөУтЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝСЎРЮ4-4ЈәЧшұкПөУлІОКэ·ҪіМ
ТФЦұҪЗЧшұкПөөДФӯөг![]() ОӘј«өгЈ¬
ОӘј«өгЈ¬ ![]() ЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ТСЦӘөг
ЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ТСЦӘөг![]() өДЦұҪЗЧшұкОӘ
өДЦұҪЗЧшұкОӘ![]() Ј¬ИфЦұПЯ
Ј¬ИфЦұПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]() ЗъПЯ
ЗъПЯ![]() өДІОКэ·ҪіМКЗ
өДІОКэ·ҪіМКЗ![]() ЈЁ
ЈЁ![]() ОӘІОКэЈ©.
ОӘІОКэЈ©.
ЈЁ1Ј©ЗуЦұПЯ![]() әНЗъПЯ
әНЗъПЯ![]() өДЖХНЁ·ҪіМЈ»
өДЖХНЁ·ҪіМЈ»
ЈЁ2Ј©ЙиЦұПЯ![]() әНЗъПЯ
әНЗъПЯ![]() Ҫ»УЪ
Ҫ»УЪ![]() БҪөгЈ¬Зу
БҪөгЈ¬Зу![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘФІ![]() әНФІ
әНФІ![]() Ј®
Ј®
ЈЁ1Ј©ЕР¶ПФІ![]() әНФІ
әНФІ![]() өДО»ЦГ№ШПөЈ»
өДО»ЦГ№ШПөЈ»
ЈЁ2Ј©№эФІ![]() өДФІРД
өДФІРД![]() ЧчФІ
ЧчФІ![]() өДЗРПЯ
өДЗРПЯ![]() Ј¬ЗуЗРПЯ
Ј¬ЗуЗРПЯ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ3Ј©№эФІ![]() өДФІРД
өДФІРД![]() Чч¶ҜЦұПЯ
Чч¶ҜЦұПЯ![]() Ҫ»ФІ
Ҫ»ФІ![]() УЪAЈ¬BБҪөгЈ®КФОКЈәФЪТФABОӘЦұҫ¶өДЛщУРФІЦРЈ¬КЗ·сҙжФЪХвСщөДФІ
УЪAЈ¬BБҪөгЈ®КФОКЈәФЪТФABОӘЦұҫ¶өДЛщУРФІЦРЈ¬КЗ·сҙжФЪХвСщөДФІ![]() Ј¬К№өГФІ
Ј¬К№өГФІ![]() ҫӯ№эөг
ҫӯ№эөг![]() ЈҝИфҙжФЪЈ¬ЗуіцФІ
ЈҝИфҙжФЪЈ¬ЗуіцФІ![]() өД·ҪіМЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
өД·ҪіМЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»ЖуТөҙУДіЙъІъПЯЙПЛж»ъійИЎ![]() јюІъЖ·Ј¬ІвБҝХвР©ІъЖ·өДДіПојјКхЦёұкЦө
јюІъЖ·Ј¬ІвБҝХвР©ІъЖ·өДДіПојјКхЦёұкЦө![]() Ј¬өГөҪөДЖөВК·ЦІјЦұ·ҪНјИзНј.
Ј¬өГөҪөДЖөВК·ЦІјЦұ·ҪНјИзНј.

ЈЁ1Ј©№АјЖёГјјКхЦёұкЦө![]() ЖҪҫщКэ
ЖҪҫщКэ![]() Ј»
Ј»
ЈЁ2Ј©ФЪЦұ·ҪНјөДјјКхЦёұкЦө·ЦЧйЦРЈ¬ТФ![]() ВдИлёчЗшјдөДЖөВКЧчОӘ
ВдИлёчЗшјдөДЖөВКЧчОӘ![]() ИЎёГЗшјдЦөөДЖөВКЈ¬Иф
ИЎёГЗшјдЦөөДЖөВКЈ¬Иф![]() Ј¬ФтІъЖ·І»әПёсЈ¬ПЦёГЖуТөГҝМмҙУёГЙъІъПЯЙПЛж»ъійИЎ
Ј¬ФтІъЖ·І»әПёсЈ¬ПЦёГЖуТөГҝМмҙУёГЙъІъПЯЙПЛж»ъійИЎ![]() јюІъЖ·јмІвЈ¬јЗІ»әПёсІъЖ·өДёцКэОӘ
јюІъЖ·јмІвЈ¬јЗІ»әПёсІъЖ·өДёцКэОӘ![]() Ј¬Зу
Ј¬Зу![]() өДКэС§ЖЪНы
өДКэС§ЖЪНы![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЎчAOBЦРЈ¬ЎПAOB=60ЎгЈ¬OA=2Ј¬OB=5Ј¬ФЪПЯ¶ОOBЙПИОИЎТ»өгCЈ¬ЎчAOCОӘ¶ЫҪЗИэҪЗРОөДёЕВККЗЈЁ Ј©
A.0.2
B.0.4
C.0.6
D.0.8
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДі№«ЛҫјЖ»®№әВт1МЁ»ъЖч,ёГЦЦ»ъЖчК№УГИэДкәујҙұ»МФМӯ.»ъЖчУРТ»ТЧЛрБгјю,ФЪ№әҪш»ъЖчКұ,ҝЙТФ¶оНв№әВтХвЦЦБгјюЧчОӘұёјю,Гҝёц200ФӘ.ФЪ»ъЖчК№УГЖЪјд,Из№ыұёјюІ»ЧгФЩ№әВт,ФтГҝёц500ФӘ.ПЦРиҫцІЯФЪ№әВт»ъЖчКұУҰН¬Кұ№әВтјёёцТЧЛрБгјю,ОӘҙЛЛСјҜІўХыАнБЛ100МЁХвЦЦ»ъЖчФЪИэДкК№УГЖЪДЪёь»»өДТЧЛрБгјюКэ,өГПВГжЦщЧҙНјЈә

јЗxұнКҫ1МЁ»ъЖчФЪИэДкК№УГЖЪДЪРиёь»»өДТЧЛрБгјюКэ,yұнКҫ1МЁ»ъЖчФЪ№әВтТЧЛрБгјюЙПЛщРиөД·СУГЈЁөҘО»ЈәФӘЈ©, ![]() ұнКҫ№ә»ъөДН¬Кұ№әВтөДТЧЛрБгјюКэ.
ұнКҫ№ә»ъөДН¬Кұ№әВтөДТЧЛрБгјюКэ.
ЈЁўсЈ©Иф![]() =19,ЗуyУлxөДәҜКэҪвОцКҪЈ»
=19,ЗуyУлxөДәҜКэҪвОцКҪЈ»
ЈЁўтЈ©ИфТӘЗуЎ°Риёь»»өДТЧЛрБгјюКэІ»ҙуУЪ![]() ЎұөДЖөВКІ»РЎУЪ0.5,Зу
ЎұөДЖөВКІ»РЎУЪ0.5,Зу![]() өДЧоРЎЦөЈ»
өДЧоРЎЦөЈ»
ЈЁўуЈ©јЩЙиХв100МЁ»ъЖчФЪ№ә»ъөДН¬КұГҝМЁ¶ј№әВт19ёцТЧЛрБгјю,»тГҝМЁ¶ј№әВт20ёцТЧЛрБгјю,·ЦұрјЖЛгХв100МЁ»ъЖчФЪ№әВтТЧЛрБгјюЙПЛщРи·СУГөДЖҪҫщКэ,ТФҙЛЧчОӘҫцІЯТАҫЭ,№әВт1МЁ»ъЖчөДН¬КұУҰ№әВт19ёц»№КЗ20ёцТЧЛрБгјюЈҝ
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com