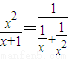练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    给出下列命题：“p：?x∈（0，+∞），不等式ax≤x2-a恒成立”；q：“1是x的不等式（x-a）（x-a-1）≤0的解”．若两命题中有且只有一个是真命题，则实数a的取值范围是    ．
    【答案】分析：通过解决二次不等式恒成立求出p是真命题时a的范围，通过解二次不等式求出q是真命题时a的范围，“有且仅有一个真”
    分两类求出a的范围．
    解答：解：若p真，则有a≤，由于在x∈（0，+∞）上是个减函数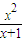，是个增函数，又当x趋向于0时，它的函数值趋向于无穷大，此时的值趋向于0，但不可能取到0，所以a≤0
    若q真则有（1-a）（1-a-1）≤0解得0≤a≤1
    ∵两命题中有且只有一个是真命题
    则①p真q假时，有a＜0
    ②p假q真时，有0＜a≤1
    综上知a∈（-∞，0）∪（0，1]
    故答案为（-∞，0）∪（0，1]
    点评：本题考查二次不等式恒成立求参数范围、二次不等式的解法、分类讨论的数学思想方法．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    11、给出下列命题：“p：?x∈（0，+∞），不等式ax≤x2-a恒成立”；q：“1是x的不等式（x-a）（x-a-1）≤0的解”．若两命题中有且只有一个是真命题，则实数a的取值范围是
    [-4，0）∪（0，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若p、q分别是M到直线l1和l2的距离，则称有序非负实数对（p，q）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列命题①若p=q=0，则“距离坐标”为（0，0）的点有且仅有1个；
    ②若p=0，q=1，则“距离坐标”为（0，1）的点有且仅有2个；
    ③若p=1，q=2，则“距离坐标”为（1，2）的点有且仅有4个．
    上述命题中，正确命题的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•朝阳区二模）给出下列命题：p：函数f（x）=sin4x-cos4x的最小正周期是π；q：?x∈R，使得log2（x+1）＜0；r：已知向量
    a
    =（λ，1），
    b
    =（-1，λ2），
    c
    =（-1，1），则（
    a
    +
    b
    ）∥
    c
    的充要条件是λ=-1．其中所有真命题是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列命题:

    ①点P为的外分点,P分所成的比λ的取值范围是(-∞,0);

    ②线段AB的一个靠近A点的三等分点分所成的比是;

    ③的定比分点P不能与P2重合,但可以与P1重合;

    ④点(x1,y1)关于坐标原点的对称点为(-y1,-x1);

    ⑤若D、E、F三点分别是△ABC三边上的中点,则△DEF与△ABC有相同的重心.

    其中正确命题的序号是____________.

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省六校教研协作体高三（上）11月联考数学试卷（文科）（解析版） 题型：选择题

    如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若p、q分别是M到直线l1和l2的距离，则称有序非负实数对（p，q）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列命题①若p=q=0，则“距离坐标”为（0，0）的点有且仅有1个；
    ②若p=0，q=1，则“距离坐标”为（0，1）的点有且仅有2个；
    ③若p=1，q=2，则“距离坐标”为（1，2）的点有且仅有4个．
    上述命题中，正确命题的个数是（ ）
    A．3
    B．2
    C．1
    D．0

    查看答案和解析>>

    同步练习册答案