
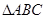 的三边长分别为
的三边长分别为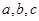 ,其内切圆半径为
,其内切圆半径为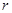 ,则三角形面积为
,则三角形面积为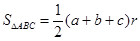 ”. 类比上述结论,拓展到空间,我们有 “若四面体
”. 类比上述结论,拓展到空间,我们有 “若四面体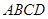 的四个面的面积分别为
的四个面的面积分别为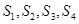 ,其内切球的半径为
,其内切球的半径为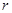 ,则四面体的体积为 ”.
,则四面体的体积为 ”. 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是自然数,所以
是自然数,所以 是整数.”以上三段推理( )。
是整数.”以上三段推理( )。| A.完全正确 |
| B.推理形式不正确 |
| C.不正确,因为两个“自然数”概念不一致 |
| D.不正确,因为两个“整数”概念不一致 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
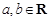 ,若
,若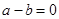 ,则
,则 ,类比得已知
,类比得已知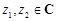 ,若
,若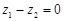 ,则
,则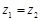 ;
;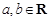 ,若
,若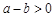 ,则
,则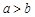 类比得已知
类比得已知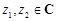 ,若
,若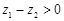 ,则
,则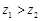 ;
; 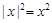 类比得复数
类比得复数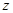 的性质
的性质 ;
; ,若复数
,若复数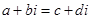 ,则
,则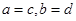 ,类比得已知
,类比得已知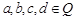 ,若
,若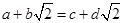 ,则
,则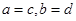 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com