
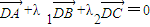 ,则∠ADB,∠BDC,∠ADC( )
,则∠ADB,∠BDC,∠ADC( )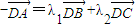 ,两边同时乘以
,两边同时乘以 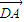 可得,-
可得,-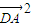 =
=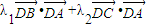 <0,故∠ADB,∠ADC中至少有一个钝角.同理可得∠ADB和∠BDC中至少有一个钝角,∠BDC和∠ADC中至少有一个钝角.从而得到∠ADB,∠BDC,∠ADC中至少有两个钝角.
<0,故∠ADB,∠ADC中至少有一个钝角.同理可得∠ADB和∠BDC中至少有一个钝角,∠BDC和∠ADC中至少有一个钝角.从而得到∠ADB,∠BDC,∠ADC中至少有两个钝角. ,∴
,∴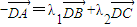 ,两边同时乘以
,两边同时乘以 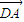 可得
可得 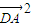 =
= <0,又 正实数λ1,λ2 ,∴∠ADB,∠ADC中至少有一个钝角.
<0,又 正实数λ1,λ2 ,∴∠ADB,∠ADC中至少有一个钝角.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com