
【题目】已知过抛物线y2=2px(p>0)的焦点的直线交抛物线于A、B两点,且|AB|= ![]() p,求AB所在的直线方程.
p,求AB所在的直线方程.
【答案】解:抛物线y2=2px(p>0)的焦点F( ![]() ,0), 设A(x1 , y1),B(x2 , y2),
,0), 设A(x1 , y1),B(x2 , y2),
若AB⊥Ox,则|AB|=2p< ![]() p,不合题意.
p,不合题意.
所以直线AB的斜率存在,设为k,
则直线AB的方程为y=k(x﹣ ![]() ),k≠0.
),k≠0.
由 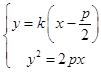 消去x,
消去x,
整理得ky2﹣2py﹣kp2=0.
由韦达定理得,y1+y2= ![]() ,y1y2=﹣p2 .
,y1y2=﹣p2 .
∴|AB|= ![]() =
= 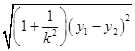 =
= 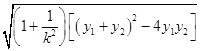 =2p(1+
=2p(1+ ![]() )=
)= ![]() p.
p.
解得k=±2.
∴AB所在的直线方程为y=2(x﹣ ![]() )或y=﹣2(x﹣
)或y=﹣2(x﹣ ![]() )
)
【解析】设A(x1 , y1),B(x2 , y2),若AB⊥Ox,则|AB|=2p< ![]() p,不合题意.所以直线AB的斜率存在,设为k,则直线AB的方程为y=k(x﹣
p,不合题意.所以直线AB的斜率存在,设为k,则直线AB的方程为y=k(x﹣ ![]() ),k≠0.联立抛物线方程,结合韦达定理和弦长公式,可得满足条件的k值,进而得到答案.
),k≠0.联立抛物线方程,结合韦达定理和弦长公式,可得满足条件的k值,进而得到答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下:
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加该项竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A、B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的大数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图1所示,B品牌的销售利润y2与投入资金x的算术平方根成正比,其关系如图2所示(利润与资金的单位:万元). 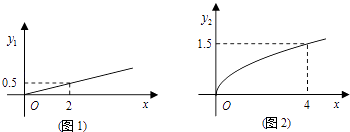
(1)分别将A、B两个品牌的销售利润y1、y2表示为投入资金x的函数关系式;
(2)该商场计划投入5万元经销该种商品,并全部投入A、B两个品牌,问:怎样分配这5万元资金,才能使经销该种商品获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an=2an-1-2n+5,(n∈N且n≥2),a1=1,
(I)若bn=an-2n+1,求证数列{bn}(n∈N*)是常数列,并求{an}的通项;
(II)若Sn是数列{an}的前n项和,又cn=(-1)nSn,且{Cn}的前n项和Tn>tn2在n∈N*时恒成立,求实数t的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com