分析:(1)以DA为x轴,以DC为y轴,以DD
1为z轴,建立空间直角坐标系,求出向量
和平面A
1ABB
1的一个法向量,利用向量法能求出直线D
1N与平面A
1ABB
1所成角的大小.
(2)分别求出向量
,
,利用向量法先求出直线CM与D
1N所成角的余弦值,再由三角函数的性质求出其正弦值.
(3)分别求出向量
和平面D
1MB的法向量,然后利用向量法能求出点N到平面D
1MB的距离.
解答: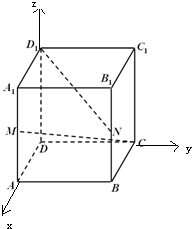
解:(1)以DA为x轴,以DC为y轴,以DD
1为z轴,建立空间直角坐标系,
∵正方体ABCD-A
1B
1C
1D
1的棱长为2,M,N分别是A
1A,B
1B的中点,
∴D
1(0,0,2),N(2,2,1),A(2,0,0),D(0,0,0)
∴
=(2,2,-1),
设直线D
1N与平面A
1ABB
1所成角为θ,
∵平面A
1ABB
1的一个法向量
=(2,0,0),
∴sinθ=|cos<
,
>|=|
|=
,
∴直线D
1N与平面A
1ABB
1所成角的大小为arcsin
.
(2)∵C(0,2,0),M(2,0,1),
∴
=(2,-2,1),
设直线CM与D
1N所成角的为α,
∵
=(2,2,-1),
∴cosθ=|cos<
,>|=|
|=
,
∴sinθ=
=
.
直线CM与D
1N所成角的正弦值为
.
(3)∵M(2,0,1),B(2,2,0),D
1(0,0,2),N(2,2,1),
∴
=(2,0,-1),
=(2,2,-2),
=(2,2,-1),
设平面D
1MB的法向量
=(x,y,z),
则
•=0,
•=0,
∴
,∴
=(1,1,2),
∴点N到平面D
1MB的距离d=
=
=
.
点评:本题考查直线与平面所成角的求法,考查点到直线的距离的求法,解题时要注意空间思维能力的培养,注意向量法的合理运用.

 如图,在棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是A1A,B1B的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是A1A,B1B的中点. 解:(1)以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
解:(1)以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,





