
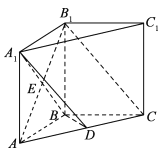
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 上的点,
上的点,![]() 平面
平面![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,且
,且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]()
【解析】
【试题分析】(1)运用线面垂直判定定理推证;(2)先求三棱锥的高与底面面积再运用三棱锥的体积公式求解:
(1)连结ED,
∵平面AB1C∩平面A1BD=ED,B1C∥平面A1BD,
∴B1C∥ED,
∵E为AB1中点,∴D为AC中点,
∵AB=BC, ∴BD⊥AC①

【法一】:由A1A⊥平面ABC,![]() 平面ABC,得A1A⊥BD②,
平面ABC,得A1A⊥BD②,
由①②及A1A、AC是平面![]() 内的两条相交直线,得BD⊥平面
内的两条相交直线,得BD⊥平面![]() .
.
【法二】:由A1A⊥平面ABC,A1A![]() 平面
平面![]()
∴平面![]() ⊥平面ABC ,又平面
⊥平面ABC ,又平面![]()
![]() 平面ABC=AC,得BD⊥平面
平面ABC=AC,得BD⊥平面![]() .
.
(2)由![]() 得BC=BB1=1,
得BC=BB1=1,
由(1)知![]() ,又
,又![]() 得
得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]()


科目:高中数学 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数 | 未损坏餐椅数 | 总计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总计 | 80 | 320 | 400 |
![]() 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
![]() 请说明是否有
请说明是否有![]() 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神
有关?![]() 参考公式:
参考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 在区间
在区间![]() 单调递减;
单调递减;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 的最大值为
的最大值为![]() .
.
其中所有正确结论的编号是( )
A.①②④B.②④C.①④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
某产品按行业生产标准分成8个等级,等级系数X依次为1,2,……,8,其中X≥5为标准A,X≥3为标准B,已知甲厂执行标准A生产该产品,产品的零售价为6元/件;乙厂执行标准B生产该产品,产品的零售价为4元/件,假定甲、乙两厂得产品都符合相应的执行标准
(I)已知甲厂产品的等级系数X1的概率分布列如下所示:

且X1的数字期望EX1=6,求a,b的值;
(II)为分析乙厂产品的等级系数X2,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数X2的数学期望.
![]() 在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
注:(1)产品的“性价比”=![]() ;
;
(2)“性价比”大的产品更具可购买性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 与函数
与函数![]() 的图像总有两个交点,设两个交点的横坐标分别为
的图像总有两个交点,设两个交点的横坐标分别为![]() ,
,![]() .
.
①求![]() 的取值范围;
的取值范围;
②求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com