
【题目】已知全集U=R,集合 ![]() ,集合
,集合 ![]() .
.
(1)求A,B;
(2)求(RA)∩B.
【答案】
(1)解:由 ![]() ≤2x<8,解得﹣1≤x<3,
≤2x<8,解得﹣1≤x<3,
∴A={x|﹣1≤x<3};
由 ![]() ,得
,得 ![]() ﹣1≥0,
﹣1≥0,
即 ![]() ≥0,
≥0,
化为(x+2)(x﹣3)≤0,且x+2≠0,
解得﹣2<x≤3,
∴B={x|﹣2<x≤3}
(2)解:由(1)可得CRA={x|x<﹣1或x≥3};
∴(CUA)∩B={x|﹣2<x<﹣1或x=3}
【解析】(1)解不等式求得集合A、B;(2)根据补集和交集的定义计算即可.
【考点精析】解答此题的关键在于理解交、并、补集的混合运算的相关知识,掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.


科目:高中数学 来源: 题型:
【题目】求满足下列条件的直线方程:
(1)求经过直线l1:x+3y﹣3=0和l2:x﹣y+1=0的交点,且平行于直线2x+y﹣3=0的直线l的方程;
(2)已知直线l1:2x+y﹣6=0和点A(1,﹣1),过点A作直线l与l1相交于点B,且|AB|=5,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(﹣∞,+∞)上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(log ![]() 3),c=f(21.6),则a,b,c的大小关系是( )
3),c=f(21.6),则a,b,c的大小关系是( )
A.c<a<b
B.c<b<a
C.b<c<a
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.已知曲线C1: ![]() (t为参数),C2:
(t为参数),C2: ![]() (θ为参数).
(θ为参数).
(1)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C2上的动点,求PQ中点M到直线C3:ρ(cosθ﹣2sinθ)=7距离的最小值.
,Q为C2上的动点,求PQ中点M到直线C3:ρ(cosθ﹣2sinθ)=7距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)=x2﹣x+b,且f(log2a)=b,log2[f(a)]=2(a≠1).
(1)求f(log2x)的最小值及对应的x值;
(2)x取何值时,f(log2x)>f(1)且log2[f(x)]<f(1)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从2009年参加奥运知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,估计这次奥运知识竞赛的及格率(大于或等于60分为及格)为 . 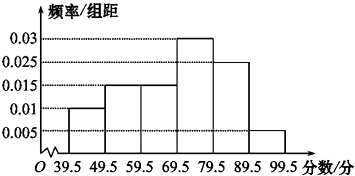
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 为集合
为集合![]() 的
的![]() 个非空子集,这
个非空子集,这![]() 个集合满足:①从中任取
个集合满足:①从中任取![]() 个集合都有
个集合都有![]()
![]()
![]() 成立;②从中任取
成立;②从中任取![]() 个集合都有
个集合都有![]()
![]() 成立.
成立.
(Ⅰ)若![]() ,
, ![]() ,
, ![]() ,写出满足题意的一组集合
,写出满足题意的一组集合![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,写出满足题意的一组集合
,写出满足题意的一组集合![]() 以及集合
以及集合![]() ;
;
(Ⅲ) 若![]() ,
, ![]() ,求集合
,求集合![]() 中的元素个数的最小值.
中的元素个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上函数f(x),且f(x)+f(﹣x)=0,当x<0时,f(x)=( ![]() )x﹣8×(
)x﹣8×( ![]() )x﹣1
)x﹣1
(1)求f(x)的解析式;
(2)当x∈[1,3]时,求f(x)的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com