
【题目】如图,在以![]() 为顶点的五面体中,O为AB的中点,
为顶点的五面体中,O为AB的中点,
![]() 平面
平面![]() ,
, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)在图中过点O作平面![]() ,使得
,使得![]() ∥平面
∥平面![]() ,并说明理由;
,并说明理由;
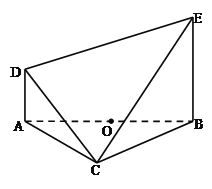
(2)求直线DE与平面CBE所成角的正切值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)在BE上取点F,使得![]() ,在BC上取点H,使
,在BC上取点H,使![]() ,平面OFH即为所求的平面
,平面OFH即为所求的平面![]() 取BE的中点G,连接AG,再证明
取BE的中点G,连接AG,再证明![]() ∥平面
∥平面![]() 即可;(2)先证明
即可;(2)先证明![]() 是
是![]() 与平面
与平面![]() 所成的角,根据
所成的角,根据![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角,利用直角三角形性质可得结果.
所成的角,利用直角三角形性质可得结果.
试题解析:(1)如图,在BE上取点F,使得![]() ,在BC上取点H,使
,在BC上取点H,使![]() ,连接OF,FH,OH,则平面OFH即为所求的平面
,连接OF,FH,OH,则平面OFH即为所求的平面![]() .
.
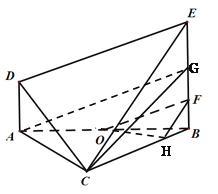
理由如下:
取BE的中点G,连接AG,
![]() ,
, ![]() 为
为![]() 中点,
中点, ![]()
![]() ∥
∥![]()
![]() ∥
∥![]() ,
, ![]() 是平行四边形,
是平行四边形,
![]()
![]() ∥
∥![]()
![]() 中,
中, ![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 中点,
中点,
所以![]() 是中位线,
是中位线,![]() ∥
∥![]()
![]() ∥
∥![]() ,
,
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() ∥平面
∥平面![]() .
.
又![]() 中,
中, ![]() ,
, ![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,即
,即![]() ∥平面
∥平面![]() .
.
(2)连接![]() ,因为
,因为![]() 平面
平面![]() ,
,
又![]() ∥
∥![]() ,所以
,所以![]() 平面
平面![]() ,
, ![]()
又![]()
![]() 平面
平面![]()
![]() 是
是![]() 与平面
与平面![]() 所成的角,
所成的角,
![]() ∥
∥![]() ,
,
![]()
![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角
所成的角
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]()
![]() 在
在![]() 中,
中, ![]()
![]() 在
在![]() 中,
中, ![]()
即直线DE与平面CBE所成角的正切值为![]()


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的方程为
的方程为![]() .
.
(Ⅰ)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() 的直角坐标为
的直角坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间中任意放置的棱长为2的正四面体![]() .下列命题正确的是_________.(写出所有正确的命题的编号)
.下列命题正确的是_________.(写出所有正确的命题的编号)
①正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() ;
;
②正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() ;
;
③正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() ;
;
④正四面体![]() 的主视图面积可能是2
的主视图面积可能是2
⑤正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两类型号,某月的产量如下表:(单位:辆). 按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
三类轿车,每类轿车均有舒适型和标准型两类型号,某月的产量如下表:(单位:辆). 按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.

(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
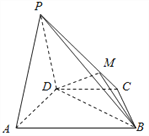
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,对于函数
为坐标原点,对于函数![]() ,称向量
,称向量![]() 为函数
为函数![]() 的伴随向量,同时称函数
的伴随向量,同时称函数![]() 为向量
为向量![]() 的伴随函数.
的伴随函数.
(Ⅰ)设函数![]() ,试求
,试求![]() 的伴随向量
的伴随向量![]() ;
;
(Ⅱ)记向量![]() 的伴随函数为
的伴随函数为![]() ,求当
,求当![]() 且
且![]() 时
时![]() 的值;
的值;
(Ⅲ)由(Ⅰ)中函数![]() 的图像(纵坐标不变)横坐标伸长为原来的
的图像(纵坐标不变)横坐标伸长为原来的![]() 倍,再把整个图像向右平移
倍,再把整个图像向右平移![]() 个单位长度得到
个单位长度得到![]() 的图像。已知
的图像。已知![]()
![]() ,问在
,问在![]() 的图像上是否存在一点
的图像上是否存在一点![]() ,使得
,使得![]() .若存在,求出
.若存在,求出![]() 点坐标;若不存在,说明理由。
点坐标;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com