
【题目】如图,矩形![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转为
翻转为![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻转过程中,有下列命题:
翻转过程中,有下列命题:
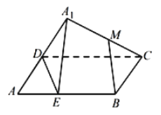
①![]() 是定值;
是定值;
②点![]() 在圆上运动;
在圆上运动;
③一定存在某个位置,使![]() ;
;
④若![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() .
.
其中正确的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:

根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,其中一个焦点与抛物线
的中心在原点,其中一个焦点与抛物线![]() 的焦点重合,点
的焦点重合,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆的左右焦点分别为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求以
,求以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知扇形的圆心角是α,半径为R,弧长为l.
(1)若α=75°,R=12 cm,求扇形的弧长l和面积;
(2)若扇形的周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国诗词大会的播出引发了全民读书热,某学校语文老师在班里开展了一次诗词默写比赛,班里40名学生得分数据的茎叶图如右图,若规定得分不低于85分的学生得到“诗词达人”的称号,低于85分且不低于70分的学生得到“诗词能手”的称号,其他学生得到“诗词爱好者”的称号.根据该次比赛的成绩按照称号的不同进行分层抽样抽选10名学生,则抽选的学生中获得“诗词能手”称号的人数为( )

A. 6B. 5C. 4D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·长沙二模)在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则![]() .推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则
.推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则![]() =________.
=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com