
| A. | (-∞,0) | B. | (0,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | $({\frac{1}{e},+∞})$ |
分析 令2017g(x)=$\frac{f(x)}{{e}^{x}}$,(x∈R),从而求导g′(x)<0,从而可判断y=g(x)单调递减,从而可得到不等式的解集.
解答 解:设2017g(x)=$\frac{f(x)}{{e}^{x}}$,由f(x)>f′(x),
得:g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$<0,
故函数g(x)在R递减,
由f(x)+2017为奇函数,得f(0)=-2017,
∴g(0)=-1,
∵f(x)+2017ex<0,∴$\frac{f(x)}{{e}^{x}}$<-2017,即g(x)<g(0),
结合函数的单调性得:x>0,
故不等式f(x)+2017ex<0的解集是(0,+∞).
故选B.
点评 本题考查了导数的综合应用及函数的性质的应用,构造函数的思想,阅读分析问题的能力,属于中档题.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:填空题
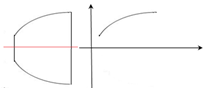 学完解析几何和立体几何后,某同学发现自己家碗的侧面可以看做抛物线的一部分曲线围绕其对称轴旋转而成,他很想知道抛物线的方程,决定把抛物线的顶点确定为原点,对称轴确定为x轴,建立如图所示的平面直角坐标系,但是他无法确定碗底中心到原点的距离,请你通过对碗的相关数据的测量以及进一步的计算,帮助他求出抛物线的方程.你需要测量的数据是碗底的直径2m,碗口的直径2n,碗的高度h(所有测量数据用小写英文字母表示),算出的抛物线标准方程为y2=$\frac{{n}^{2}-{m}^{2}}{h}$x.
学完解析几何和立体几何后,某同学发现自己家碗的侧面可以看做抛物线的一部分曲线围绕其对称轴旋转而成,他很想知道抛物线的方程,决定把抛物线的顶点确定为原点,对称轴确定为x轴,建立如图所示的平面直角坐标系,但是他无法确定碗底中心到原点的距离,请你通过对碗的相关数据的测量以及进一步的计算,帮助他求出抛物线的方程.你需要测量的数据是碗底的直径2m,碗口的直径2n,碗的高度h(所有测量数据用小写英文字母表示),算出的抛物线标准方程为y2=$\frac{{n}^{2}-{m}^{2}}{h}$x.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
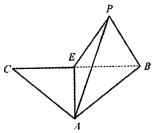 等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.
等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{{\root{3}{4}}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{{\root{3}{4}}}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
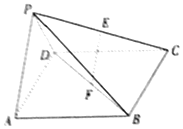 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
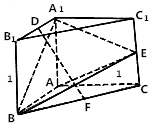 已知三棱柱ABC-A1B1C1中,底面三角形ABC是直角三角形,四边形A1ACC1和四边形A1ABB1均为正方形,D,E,F分别是A1B1,C1C,BC的中点,AB=1.
已知三棱柱ABC-A1B1C1中,底面三角形ABC是直角三角形,四边形A1ACC1和四边形A1ABB1均为正方形,D,E,F分别是A1B1,C1C,BC的中点,AB=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com