练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，设椭圆： 的离心率为， 分别为椭圆的左、右顶点， 为右焦点，直线与的交点到轴的距离为，过点作轴的垂线， 为上异于点的一点，以为直径作圆.

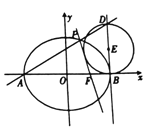
    （1）求的方程；

    （2）若直线与的另一个交点为，证明：直线与圆相切.

    【答案】(1) ；(2)证明见解析.

    【解析】试题分析：

    (1)结合题意可求得， ，则的方程为.

    (2)由题意可得，直线与圆相切时，直线的斜率为，结合(1)中求得的椭圆方程即可证得题中的结论.

    试题解析：

    （1）解：由题可知， ，∴， ，

    设椭圆的方程为，

    由，得，∴， ， ，

    故的方程为.

    （2）证明：由（1）可得： ，设圆的圆心为，则，

    圆的半径为，

    直线的方程为.

    设过与圆相切的直线方程为，

    则，整理得： ，

    由，得，

    又∵，

    ∴直线与圆相切.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在几何体中，四边形是矩形， 平面， . ， 分别是线段的中点.

    （Ⅰ）求证： 平面；

    （Ⅱ）求与平面所成角的正切值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设点是棱长为2的正方体的棱的中点，点在面所在的平面内，若平面分别与平面和平面所成的锐二面角相等，则点到点的最短距离是（ ）

    A. B. C. 1 D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（ex）=ax2﹣x，a∈R．
    （1）求f（x）的解析式；
    （2）求x∈（0，1]时，f（x）的值域；
    （3）设a＞0，若h（x）=[f（x）+1﹣a]logxe对任意的x1 ， x2∈[e﹣3 ， e﹣1]，总有|h（x1）﹣h（x2）|≤a+ 恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某机构为了解某地区中学生在校月消费情况，随机抽取了100名中学生进行调查．如图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图．已知[350，450），[450，550），[550，650）三个金额段的学生人数成等差数列，将月消费金额不低于550元的学生称为“高消费群”．

    （1）求m，n的值，并求这100名学生月消费金额的样本平均数 （同一组中的数据用该组区间的中点值作代表）；
    （2）根据已知条件完成下面2×2列联表，并判断能否有90%的把握认为“高消费群”与性别有关？

    高消费群

    非高消费群

    合计

    男

    女

    10

    50

    合计

    （参考公式： ，其中n=a+b+c+d）

    P（K2≥k）

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，若输出的 ，则判断框内填入的条件可以是（ ）
    A.k≥7
    B.k＞7
    C.k≤8
    D.k＜8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场在店庆一周年开展“购物折上折活动”：商场内所有商品按标价的八折出售，折后价格每满500元再减100元．如某商品标价为1500元，则购买该商品的实际付款额为1500×0.8﹣200=1000（元）．设购买某商品得到的实际折扣率= ．设某商品标价为x元，购买该商品得到的实际折扣率为y．
    （1）写出当x∈（0，1000]时，y关于x的函数解析式，并求出购买标价为1000元商品得到的实际折扣率；
    （2）对于标价在[2500，3500]的商品，顾客购买标价为多少元的商品，可得到的实际折扣率低于 ？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】曲线的参数方程为 (为参数)，以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.

    (1)写出的直角坐标方程，并且用 (为直线的倾斜角， 为参数)的形式写出直线的一个参数方程；

    (2) 与是否相交，若相交求出两交点的距离，若不相交，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】规定投掷飞镖3次为一轮，若3次中至少两次投中8环以上为优秀，现采用随机模拟实验的方法估计某人投掷飞镖的情况：先由计算器产生随机数0或1，用0表示该次投标未在8环以上，用1表示该次投标在8环以上；再以每三个随机数作为一组，代表一轮的结果，经随机模拟实验产生了如下20组随机数：

    101 111 011 101 010 100 100 011 111 110

    000 011 010 001 111 011 100 000 101 101

    据此估计，该选手投掷飞镖三轮，至少有一轮可以拿到优秀的概率为（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案