
 ��ͼ����֪������y=ax2+bx+c����O��0��0����A��4��0����B��3��$\sqrt{3}$�����㣬����AB������B��BC��x�ύ���������ڵ�C��
��ͼ����֪������y=ax2+bx+c����O��0��0����A��4��0����B��3��$\sqrt{3}$�����㣬����AB������B��BC��x�ύ���������ڵ�C������ ��1�����ô���ϵ����������O��A��B���ⷽ�̿ɵ�a��b��c�������õ������ߵķ��̣�
��2���ٹ�B��BE��ֱ��x�ᣬ����Q��QF��x�ύx����F���ֱ����PA��QF�ij������������ε������ʽ�����ɵõ�����
���ɶ��κ�������ֵ�������ɵõ��������ֵ��������PQA����״��
��3�����ڣ�����Q��AB���˶�ʱ��Ҫʹ�á�PQA��ֱ�ǡ�������ʹ��PQA=90�㣮��ֱ�������ε����ʼ��ɵõ�����t��ֵ���Լ�P��Q�����꣮
��� 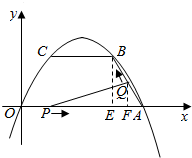 �⣺��1��������y=ax2+bx+c����O��0��0����A��4��0����
�⣺��1��������y=ax2+bx+c����O��0��0����A��4��0����
B��3��$\sqrt{3}$�����㣬
��$\left\{\begin{array}{l}16a+4b+c=0\\ 9a+3b+c=\sqrt{3}\end{array}\right.���a=-\frac{{\sqrt{3}}}{3}��b=\frac{{4\sqrt{3}}}{3}��c=0$��
��$y=-\frac{{\sqrt{3}}}{3}{x^2}+\frac{{4\sqrt{3}}}{3}x$��
��2��
�ٹ�B��$BE��x��x����E����BE=\sqrt{3}��AE=1��AB=2$��
$��tan��BAE=\frac{BE}{AE}=\sqrt{3}�á�BAE=6{0^0}$
������QA=t��PA=4-t��
����Q��QF��x�ύx����F��
��$sin��BAE=\frac{QF}{AQ}��QF=\frac{{\sqrt{3}t}}{2}$��
��S=$\frac{1}{2}$PA•QF=$\frac{1}{2}��4-t��•\frac{{\sqrt{3}}}{2}t$=$-\frac{{\sqrt{3}}}{4}{t^2}+\sqrt{3}t$=$-\frac{{\sqrt{3}}}{4}{��t-2��^2}+\sqrt{3}$��
����S=-$\frac{\sqrt{3}}{4}$��t-2��2+$\sqrt{3}$����-$\frac{\sqrt{3}}{4}$��0���ɵõ�t=2ʱ��Sȡ�����ֵ$\sqrt{3}$��
��ʱ��PQA�ǵȱ������Σ�
��3�����ڣ�����Q��AB���˶�ʱ��
Ҫʹ�á�PQA��ֱ�ǡ�������ʹ��PQA=90�㣮
��PA=2QA��
��4-t=2t��
��$t=\frac{4}{3}$��
��P��$\frac{4}{3}$��0����Q��$\frac{10}{3}$��$\frac{2\sqrt{3}}{3}$����
���� ���⿼����κ����Ľ���ʽ����ע�����ô���ϵ���������������ε������ʽ�����ã��Լ�ֱ�������ε��жϣ�ע�����ö��κ�������ֵ�����������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | -2 | C�� | 2 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
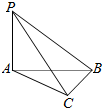 ��ͼ��Rt��ABC�У���ACB=90�㣬��BAC=45�㣬PA��ƽ��ABC����PA=BC=1��������A-PB-C��ƽ�����60�㣮
��ͼ��Rt��ABC�У���ACB=90�㣬��BAC=45�㣬PA��ƽ��ABC����PA=BC=1��������A-PB-C��ƽ�����60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{8}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3e | B�� | -1 | C�� | -e3 | D�� | e2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��0 | B�� | x��0 | C�� | x��2 | D�� | x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com