
【题目】直角坐标系xOy平面内,已知动点M到点D(﹣4,0)与E(﹣1,0)的距离之比为2.
(1)求动点M的轨迹C的方程;
(2)是否存在经过点(﹣1,1)的直线l,它与曲线C相交于A,B两个不同点,且满足 ![]() (O为坐标原点)关系的点M也在曲线C上,如果存在,求出直线l的方程;如果不存在,请说明理由.
(O为坐标原点)关系的点M也在曲线C上,如果存在,求出直线l的方程;如果不存在,请说明理由.
【答案】
(1)解:设M(x,y),则 ![]() ,
, ![]() ,
,
依题意, ![]() ,
,
化简整理,得x2+y2=4,
∴曲线c的方程为x2+y2=4.
(2)解:假设直线l存在,设A(x1,y1),B(x2,y2),M(x0,y0)
①若直线l的斜率存在,设直线l的方程为:y﹣1=k(x+1).
联立 ![]() 消去y得,(1+k2)x2+2k(k+1)x+k2+2k﹣3=0,
消去y得,(1+k2)x2+2k(k+1)x+k2+2k﹣3=0,
由韦达定理得, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
∵点A(x1,y1),B(x2,y2)在圆c上,
∴ ![]() ,
, ![]() .
.
由 ![]() 得,
得, ![]() ,
, ![]() .
.
由于点M也在圆c上,则 ![]() ,
,
整理得, ![]() +
+ ![]() ,
,
即x1x2+y1y2=0,所以 ![]() +
+ ![]() ,
,
从而得,k2﹣2k+1=0,即k=1,因此,直线l的方程为y﹣1=x+1,即x﹣y+2=0;
②若直线l的斜率不存在,则A(﹣1, ![]() ),B(﹣1,-
),B(﹣1,- ![]() ),
), ![]() ,故此时点M不在曲线c上,
,故此时点M不在曲线c上,
综上所知:k=1,直线方程为x﹣y+2=0.
【解析】(1)设出M点的坐标,由题目条件即可得出动点M的轨迹C的方程;(2)讨论直线l的斜率是否存在,由韦达定理,根据题目条件进行计算即可.


科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D. 
(1)求证:CE2=CDCB.
(2)若AB=2,BC= ![]() ,求CE与CD的长.
,求CE与CD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位安排![]() 位员工在春节期间大年初一到初七值班,每人值班
位员工在春节期间大年初一到初七值班,每人值班![]() 天,若
天,若![]() 位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有( )
位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】试题分析:(1)设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() ,由已知条件求出
,由已知条件求出![]() ,再写出通项公式;(2)由
,再写出通项公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
试题解析:设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,结合
,结合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
【题型】解答题
【结束】
20
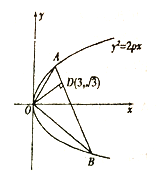
【题目】如图,已知直线与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 为抛物线上任一点,求
为抛物线上任一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点F. 
(1)证明:PB∥平面AEC;
(2)若ABCD为正方形,探究在什么条件下,二面角C﹣AF﹣D大小为60°?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某种商品在过去50天的销量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N),前30天价格为g(t)=![]() t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
(1)写出该种商品的日销售额S与时间t的函数关系式;
(2)求日销售额S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)分别计算两个样本的平均数![]() 和标准差
和标准差![]() ,并根据计算结果估计哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com