
(本题满分14分,第1小题6分,第2小题8分)
已知函数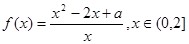 ,其中常数a > 0.
,其中常数a > 0.
(1) 当a = 4时,证明函数f(x)在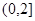 上是减函数;
上是减函数;
(2) 求函数f(x)的最小值.
(1)任取0<x1<x2≤2,则f(x1)–f(x2)=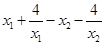
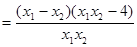 ,
,
因为0<x1<x2≤2,所以f(x1)–f(x2)>0,即f(x1)>f(x2);
(2)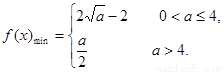 。
。
【解析】
试题分析:(1) 当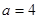 时,
时,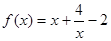 ,…………………………………………1分
,…………………………………………1分
任取0<x1<x2≤2,则f(x1)–f(x2)=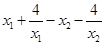
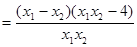 ………………3分
………………3分
因为0<x1<x2≤2,所以f(x1)–f(x2)>0,即f(x1)>f(x2)………………………………………5分
所以函数f(x)在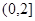 上是减函数;………………………………………………………6分
上是减函数;………………………………………………………6分
(2)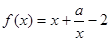
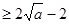 ,……………………………………………………7分
,……………………………………………………7分
当且仅当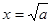 时等号成立,…………………………………………………………8分
时等号成立,…………………………………………………………8分
当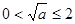 ,即
,即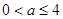 时,
时,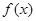 的最小值为
的最小值为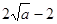 ,………………………10分
,………………………10分
当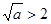 ,即
,即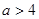 时,
时,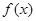 在
在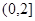 上单调递减,…………………………………11分
上单调递减,…………………………………11分
所以当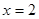 时,
时,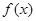 取得最小值为
取得最小值为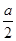 ,………………………………………………13分
,………………………………………………13分
综上所述: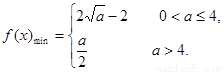 ………………………………………14分
………………………………………14分
考点:函数的单调性和最值;基本不等式。
点评:用定义法证明函数单调性的步骤:一设二作差三变形四判断符号五得出结论,其中最重要的是四变形,最好变成几个因式乘积的形式,这样便于判断符号。


科目:高中数学 来源: 题型:
(本题满分14分,第(1)小题6分,第(2)小题8分)
四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60![]() ,在四边形ABCD中,∠ADC=∠DAB=90
,在四边形ABCD中,∠ADC=∠DAB=90![]() ,AB=4,CD=1,AD=2.
,AB=4,CD=1,AD=2.

(1)求四棱锥P-ABCD的体积;
(2)求异面直线PA与BC所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分,第(1)小题4分,第(2)小题4分,第(2)小题6分)
设数列![]() 中,若
中,若![]() ,则称数列
,则称数列![]() 为“凸数列”。
为“凸数列”。
(1)设数列![]() 为“凸数列”,若
为“凸数列”,若![]() ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;
(2)在“凸数列”![]() 中,求证:
中,求证:![]() ;
;
(3)设![]() ,若数列
,若数列![]() 为“凸数列”,求数列前
为“凸数列”,求数列前![]() 项和
项和![]() 。
。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市金山区高三上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分14分,第1小题6分,第2小题8分)
已知函数 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1.
(1) 求m的值,并求f(x)的单调递增区间;
(2) 在△ABC中,角A、B、C的对边a、b、c,若 ,且
,且 ,试判断△ABC的形状.
,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市高三上学期期中考试数学卷 题型:解答题
(本题满分14分,第1小题5分,第2小题9分)
一校办服装厂花费2万元购买某品牌运动装的生产与销售权,根据以往经验,每生产1百套这种品牌运动装的成本为1万元,每生产x(百套)的销售额R(x)(万元)满足:

(1)该服装厂生产750套此种品牌运动装可获得利润多少万元?
(2)该服装厂生产多少套此种品牌运动装利润最大?此时,利润是多少万元?
查看答案和解析>>
科目:高中数学 来源:上海市长宁区2010届高三第二次模拟考试数学文 题型:解答题
(本题满分14分,第(1)小题6分,第(2)小题8分)
设函数 ,若不等式
,若不等式 的解集为
的解集为 。
。
(1)求 的值;
的值;
(2)若函数 在
在 上的最小值为1,求实数
上的最小值为1,求实数 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com