
【题目】下表是某原料在市场上从2013年至2019年这7年中每年的平均价格(单位:千元/吨)数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
平均价格 (单位:千元/吨) |
|
|
|
|
|
|
|
(![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程(系数精确到
为预报变量的线性回归方程(系数精确到![]() );
);
(2)以(1)的结论为依据,预测2032年该原料价格.预估该原料价格在哪一年突破1万元/吨?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: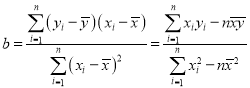 ,
,![]() .
.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】纹样是中国传统文化的重要组成部分,它既代表着中华民族的悠久历史、社会的发展进步,也是世界文化艺术宝库中的巨大财富.小楠从小就对纹样艺术有浓厚的兴趣.收集了如下9枚纹样微章,其中4枚凤纹徽章,5枚龙纹微章.小楠从9枚徽章中任取3枚,则其中至少有一枚凤纹徽章的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中有16个格点(i,j),其中0≤i≤3,0≤j≤3.若在这16个点中任取n个点,这n个点中总存在4个点,这4个点是一个正方形的顶点,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆锥PO中,AB是圆O的直径,且AB=4,C是底面圆O上一点,且AC=2![]() ,点D为半径OB的中点,连接PD.
,点D为半径OB的中点,连接PD.
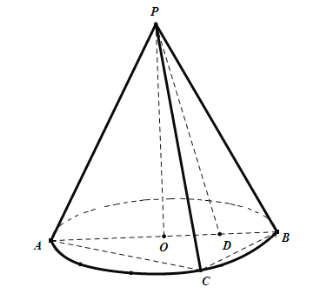
(1)求证:PC在平面APB内的射影是PD;
(2)若PA=4,求底面圆心O到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,
,![]() 上的点
上的点![]() 与
与![]() 的两个焦点所构成的三角形的周长为
的两个焦点所构成的三角形的周长为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() ∥
∥![]() .判断
.判断![]() 是否为定值,若是求出该值;若不是请说明理由.
是否为定值,若是求出该值;若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线C1:x=﹣2以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,C2极坐标方程为:ρ2﹣2ρcosθ﹣4ρsinθ+4=0.
(1)求C1的极坐标方程和C2的普通方程;
(2)若直线C3的极坐标方程为![]() ,设C2与C3的交点为M,N,又C1:x=﹣2与x轴交点为H,求△HMN的面积.
,设C2与C3的交点为M,N,又C1:x=﹣2与x轴交点为H,求△HMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的左、右焦点
的左、右焦点![]() 分别作倾斜角为
分别作倾斜角为![]() 的直线
的直线![]() ,且
,且![]() 之间的距离为1.
之间的距离为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 只有一个公共点,求点
只有一个公共点,求点![]() 到直线
到直线![]() 的距离之积.
的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,抛物线
,抛物线![]() 上存在一点M,使得直线AM的斜率的最大值为1,圆Q的方程为
上存在一点M,使得直线AM的斜率的最大值为1,圆Q的方程为![]() .
.
(1)求点M的坐标和C的方程;
(2)若直线l交C于D,E两点且直线MD,ME都与圆Q相切,证明直线l与圆Q相离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com