
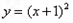 与圆
与圆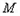 :
: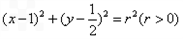 有一个公共点
有一个公共点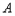 ,且在
,且在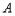 处两曲线的切线为同一直线上。
处两曲线的切线为同一直线上。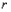 ;
;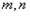 是异于
是异于 且与
且与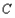 及
及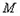 都切的两条直线,
都切的两条直线,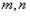 的交点为
的交点为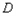 ,求
,求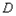 到
到 的距离。
的距离。科目:高中数学 来源: 题型:
 | ACB |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)(注意:在试题卷上作答无效)
已知抛物线C:![]() 与圆
与圆![]() 有一个公共点A,且在A处两曲线的切线与同一直线
有一个公共点A,且在A处两曲线的切线与同一直线![]()
(I) 求r;
(II) 设m、n是异于![]() 且与C及M都相切的两条直线,m、n的交点为D,求D到
且与C及M都相切的两条直线,m、n的交点为D,求D到![]() 的距离。
的距离。
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试文科数学(大纲卷解析版) 题型:解答题
已知抛物线C: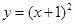 与圆
与圆 有一个公共点A,且在A处两曲线的切线与同一直线l
有一个公共点A,且在A处两曲线的切线与同一直线l
(I) 求r;
(II) 设m、n是异于l且与C及M都相切的两条直线,m、n的交点为D,求D到l的距离。
【解析】本试题考查了抛物线与圆的方程,以及两个曲线的公共点处的切线的运用,并在此基础上求解点到直线的距离。
【点评】该试题出题的角度不同于平常,因为涉及的是两个二次曲线的交点问题,并且要研究两曲线在公共点出的切线,把解析几何和导数的工具性结合起来,是该试题的创新处。另外对于在第二问中更是难度加大了,出现了另外的两条公共的切线,这样的问题对于我们以后的学习也是一个需要练习的方向。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com