
【题目】已知函数![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)如果对任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)(-![]() ,2]
,2]
【解析】
(1)将a代入,求出函数的导数,分别解f′(x)〈0和f′(x)〉0,求出函数的单调区间即可;
(2)由原不等式移项为右侧为0的形式,构造新的函数,通过求导对a讨论,研究其增减性及最值,逐步得解.
(1)当a=2时,f(x)=(x2+2x+1)e-x
f′(x)=-(x+1)(x-1)e-x
由f′(x)〈0得x<-1或x>1;由f′(x)〉0得-1<x<1;
所以f(x)的单调递增区间为(-1,1),
f(x)的单调递减区间为(-![]() ,-1),(1,+
,-1),(1,+![]() )
)
(2)f(x)≤x+1
![]() ax2+ax+1≤(x+1)ex
ax2+ax+1≤(x+1)ex
(x+1)ex-![]() ax2-ax-1≥0
ax2-ax-1≥0
令g(x)=(x+1)ex-![]() ax2-ax-1,则g′(x)=(x+2)ex-ax-a,
ax2-ax-1,则g′(x)=(x+2)ex-ax-a,
令F(x)=g′(x)=(x+2)ex-ax-a,则F′(x)=(x+3)ex-a,
令t(x)=F′(x)=(x+3)ex-a,则t′(x)=(x+4) ex,
当x≥0时,t′(x)>0恒成立,从而t(x)在[0,+![]() )上单调递增,
)上单调递增,
此时t(0)=3-a,
F(0)=2-a,g(0)=0
当a≤2时,t(x)≥t(0)=3-a>0,即F′(x)>0所以F(x)在[0,+![]() )上单调递增
)上单调递增
所以F(x)≥F(0)=2-a≥0,即g′(x)≥0,从而g(x)在[0,+![]() )上单调递增
)上单调递增
所以g(x)≥g(0)=0
即(x+1)ex-![]() ax2-ax-1≥0恒成立,
ax2-ax-1≥0恒成立,
所以当a≤2时合题意;
②当2<a≤3时,t(x)在[0,+![]() )上单调递增,且t(x)≥t(0)=3-a≥0即F′(x)≥0
)上单调递增,且t(x)≥t(0)=3-a≥0即F′(x)≥0
∴F(x)=g′(x)在[0,+![]() )上单调递增,又F(0)=g′(0)=2-a<0,
)上单调递增,又F(0)=g′(0)=2-a<0,
∴必存在x1(0,+![]() ),使得x
),使得x![]() (0,x1)时,
(0,x1)时,
g(x)在(0,x1)上单调递减,
∴g(x)<g(0)=0,
这与g(x)≥0在x≥0时恒成立矛盾,从而当2<a≤3时不合题意;
③当a>3时,t(x)在[0,+![]() )上单调递增且t(0)=3-a<0,
)上单调递增且t(0)=3-a<0,
必存在x2(0,+![]() ),使得x(0,x2)时,t(x)<0,即F′(x)<0,从而F(x)=g′(x)在[0,+
),使得x(0,x2)时,t(x)<0,即F′(x)<0,从而F(x)=g′(x)在[0,+![]() )上单调递减,
)上单调递减,
∴F(x)<F(0)=g′(0)=2-a<0,
从而g(x)在(0,x1)上单调递减 ,
g(x)<g(0)=0,这与g(x)≥0在x≥0时恒成立矛盾,从而a>3时不合题意;
综上:a的取值范围是(-![]() ,2]
,2]


科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 | 1 | 2 | 3 | 4 | 5 |
管理时间 | 8 | 10 | 13 | 25 | 24 |
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?
(3)若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
参考公式:
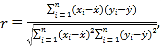
![]()
其中![]() 。临界值表:
。临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,三个点
,三个点![]() ,
, ![]() ,
, ![]() 中恰有两个点在
中恰有两个点在![]() 上.
上.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的直线交
的直线交![]() 于
于![]() ,
, ![]() 两点,点
两点,点![]() 为
为![]() 上任意一点,证明:直线
上任意一点,证明:直线![]() ,
, ![]() ,
, ![]() 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是某地区不同身高的未成年男性的体重平均值表.
身高/ | 60 | 70 | 80 | 90 | 100 | 110 |
体重/ | 6.13 | 7.9 | 9.99 | 12.15 | 15.02 | 17.5 |
身高/ | 120 | 130 | 140 | 150 | 160 | 170 |
体重/ | 20.92 | 26.86 | 31.11 | 38.85 | 42.25 | 55.05 |
(1)给出两个回归方程:
①![]() ,②
,②![]() .通过计算,得到它们的相关指数分别是:
.通过计算,得到它们的相关指数分别是:![]() ,
,![]() .试问哪个回归方程拟合效果更好?
.试问哪个回归方程拟合效果更好?
(2)若体重超过相同身高男性平均值的1.2倍为偏胖,低于0.8为偏瘦,那么该地区某中学一男生身高为![]() ,体重为
,体重为![]() ,他的体重是否正常?
,他的体重是否正常?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,椭圆
成等比数列,椭圆![]() 上的点到焦点
上的点到焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() 过该椭圆的右焦点作两条互相垂直的弦
过该椭圆的右焦点作两条互相垂直的弦![]() 与
与![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com