
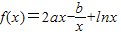 在x=1和
在x=1和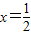 处取得极值.
处取得极值.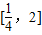 上存在x,使得不等式f(x)-c≤0成立,求实数c的最小值.(参考数据e2≈7.389,e3≈20.08)
上存在x,使得不等式f(x)-c≤0成立,求实数c的最小值.(参考数据e2≈7.389,e3≈20.08) 在x=1和
在x=1和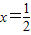 处取得极值,我们求出函数的导函数f′(x)的解析式,易得
处取得极值,我们求出函数的导函数f′(x)的解析式,易得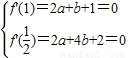 ,解方程组,即可得到实数a,b的值;
,解方程组,即可得到实数a,b的值;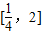 上存在x,使得不等式f(x)-c≤0成立,表示函数f(x)在区间
上存在x,使得不等式f(x)-c≤0成立,表示函数f(x)在区间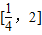 上的最小值小于等于c,根据(1)中函数的解析式,求出函数f(x)在区间
上的最小值小于等于c,根据(1)中函数的解析式,求出函数f(x)在区间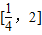 上的最小值,即可得到答案.
上的最小值,即可得到答案.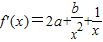 …(2分)
…(2分)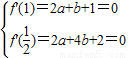 ,解得,
,解得,
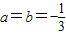 …(5分)
…(5分)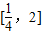 上存在x,使不等式f(x)-c≤0成立,只需c≥[f(x)]min
上存在x,使不等式f(x)-c≤0成立,只需c≥[f(x)]min
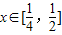 时,f′(x)<0,故函数f(x)在
时,f′(x)<0,故函数f(x)在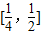 上单调递减,
上单调递减,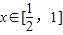 时,f′(x)>0,故函数f(x)在
时,f′(x)>0,故函数f(x)在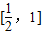 上单调递增,
上单调递增,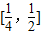 上单调递减…(7分)
上单调递减…(7分)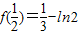 是f(x)在
是f(x)在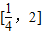 上的极小值,且函数f(x)的最小值必是
上的极小值,且函数f(x)的最小值必是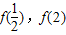 两者中较小的…(8分)
两者中较小的…(8分)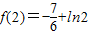 ,
,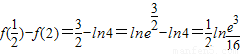 ∵e3≈20.08>16,
∵e3≈20.08>16,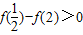 ∴
∴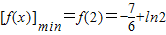 …(9分)∴
…(9分)∴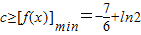
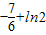 .…(10分)
.…(10分)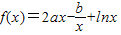 在x=1和
在x=1和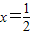 处取得极值,构造关于a,b的方程,确定出函数f(x)的解析式,是解答本题的关键.
处取得极值,构造关于a,b的方程,确定出函数f(x)的解析式,是解答本题的关键. 

科目:高中数学 来源: 题型:解答题
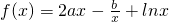 在x=1和
在x=1和 处取得极值.
处取得极值.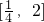 上存在x0,使得不等式f(x0)-c≤0成立,求实数c的最小值.(参考数据e2≈7.389,e3≈20.08)
上存在x0,使得不等式f(x0)-c≤0成立,求实数c的最小值.(参考数据e2≈7.389,e3≈20.08)查看答案和解析>>
科目:高中数学 来源:2009-2010学年吉林省长春市东北师大附中高二(上)期末数学试卷(文科)(解析版) 题型:解答题
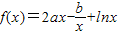 在x=1和
在x=1和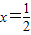 处取得极值.
处取得极值. 上存在x,使得不等式f(x)-c≤0成立,求实数c的最小值.(参考数据e2≈7.389,e3≈20.08)
上存在x,使得不等式f(x)-c≤0成立,求实数c的最小值.(参考数据e2≈7.389,e3≈20.08)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com