
分析 (1)由条件:“x∈Z”知集合A中的元素是整数,进而求它的子集的个数;
(2)由条件:“B=∅”知集合B中的没有任何元素是,得不等式的解集是空集,进而求m;
(3)由条件:“A?B”知集合B是A的子集,结合端点的不等关系列出不等式后解之即得.
解答 解:化简集合A={x|-2≤x≤5},集合B可写为B={x|(x-m+1)(x-2m-1)<0}
(1)∵x∈Z,∴A={-2,-1,0,1,2,3,4,5},即A中含有8个元素,
∴A的非空真子集数为28-2=254(个).
(2)显然只有当m-1=2m+1即m=-2时,B=∅.
(3)当B=∅即m=-2时,B=∅⊆A;
当B≠∅即m≠-2时,
(ⅰ)当m<-2时,B=(2m+1,m-1),要B⊆A,只要$\left\{\begin{array}{l}{2m+1≥-2}\\{m-1≤5}\end{array}\right.$,∴-$\frac{3}{2}$≤m≤6,∴m的值不存在;
(ⅱ)当m>-2时,B=(m-1,2m+1),要B⊆A,只要$\left\{\begin{array}{l}{m-1≥-2}\\{2m+1≤5}\end{array}\right.$,∴-1≤m≤2.
综上所述,m=-2,或-1≤m≤2.
点评 本题考查集合的子集、集合的包含关系判断及应用以及空集的性质及运算.是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | M=∅,N={0} | B. | M={2,3},N={(2,3)} | ||
| C. | M={x|y=x+1},N={y|y=x+1,x∈R} | D. | M={(x,y)|y=-x2+5},N={y=-x2+5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
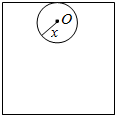 如图,半径为r的圆O在边长为4的正方形内与正方形一边相切并滚动一周后,圆O没有通过区域的面积为S.
如图,半径为r的圆O在边长为4的正方形内与正方形一边相切并滚动一周后,圆O没有通过区域的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com