[题目]在直角坐标系中.曲线的参数方程为为参数..直线的参数方程为为参数)．(1)若与相交.求实数的取值范围,(2)若.设点在曲线上.求点到的距离的最大值.并求此时点的坐标．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】在直角坐标系中，曲线的参数方程为为参数，，直线的参数方程为为参数）．

（1）若与相交，求实数的取值范围；

（2）若，设点在曲线上，求点到的距离的最大值，并求此时点的坐标．

【答案】（1）；（2）最大值为，此时点坐标为.

【解析】

（1）利用参数方程与普通方程的互化公式求出曲线和直线的普通方程，将与的方程联立得到关于的一元二次方程，根据题意，利用方程的判别式求解即可；

（2）由（1）可知的普通方程，设点，利用点到直线的距离公式和辅助角公式求出点到的距离的最大值，结合之间的关系，利用诱导公式求出此时的值即可求出点的坐标.

（1）由题意可知，曲线的普通方程为，

直线的普通方程为，

将与的方程联立，得，

因为与相交，所以，

整理得，解得，

所以实数的取值范围是．

（2）当时，的普通方程为，

设点，则点到的距离为

，

其中，又因为，

所以当即时，，

所以，

，所以．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某支上市股票在30天内每股的交易价格（单位：元）与时间（单位：天）组成有序数对，点落在如图所示的两条线段上.该股票在30天内（包括30天）的日交易量（单位：万股）与时间（单位：天）的部分数据如下表所示：

第天	4	10	16	22
（万股）	36	30	24	18

（Ⅰ）根据所提供的图象，写出该种股票每股的交易价格与时间所满足的函数解析式；

（Ⅱ）根据表中数据确定日交易量与时间的一次函数解析式；

（Ⅲ）若用（万元）表示该股票日交易额，请写出关于时间的函数解析式，并求出在这30天中，第几天的日交易额最大，最大值是多少？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数，，其中

若函数，存在相同的零点，求a的值

若存在两个正整数m，n，当时，有与同时成立，求n的最大值及n取最大值时a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知下列四个说法中：

①与表示同一函数；

②已知函数的定义域为，则的定义域为；

③不等式对于恒成立，则的取值范围是；

④对于集合，，

若，则的取值范围，其中正确说法的序号是______．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】十九大指出中国的电动汽车革命早已展开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的计划．2018年某企业计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本2500万元，每生产x（百辆），需另投入成本万元，且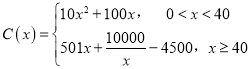．由市场调研知，每辆车售价5万元，且全年内生产的车辆当年能全部销售完．