
分析 根据数列递推关系,建立方程,利用构造法得到数列{an+1-3an}是公比q=2的等比数列,求出其通项公式后两边同时除以3n+1,然后利用累加法求得数列an的通项公式,进一步得到bn的通项公式.
解答 解:∵a1=2,b1=4,
∴a2=-a1-2b1=-2-8=-10,
由an+1=-an-2bn,得an+1+an=-2bn,
∵bn+1=6an+6bn,
∴bn+1=6an-3an+1-3an=-3an+1+3an,
即an+2+an+1=-2bn+1=-2(-3an+1+3an),
即an+2=5an+1-6an,
则an+2-3an+1=2(an+1-3an),
即数列{an+1-3an}是公比q=2的等比数列,首项为a2-3a1=-16,
则an+1-3an=-2n+3,
两边同除以3n+1,得$\frac{{a}_{n+1}}{{3}^{n+1}}-\frac{{a}_{n}}{{3}^{n}}=-\frac{{2}^{n+3}}{{3}^{n+1}}$=-4×($\frac{2}{3}$)n+1,
则$\frac{{a}_{2}}{{3}^{2}}-\frac{{a}_{1}}{3}$=-4×($\frac{2}{3}$)2,
$\frac{{a}_{3}}{{3}^{3}}-\frac{{a}_{2}}{{3}^{2}}$=-4×($\frac{2}{3}$)3,
…
$\frac{{a}_{n}}{{3}^{n}}-\frac{{a}_{n-1}}{{3}^{n-1}}$=-4×($\frac{2}{3}$)n-1,
等式两边同时相加得$\frac{{a}_{n}}{{3}^{n}}-\frac{{a}_{1}}{3}$=-4×$\frac{\frac{4}{9}-(\frac{2}{3})^{n+1}}{1-\frac{2}{3}}$,
∴$\frac{{a}_{n}}{{3}^{n}}=\frac{{a}_{1}}{3}$-4×$\frac{\frac{4}{9}-(\frac{2}{3})^{n+1}}{1-\frac{2}{3}}$=3×($\frac{2}{3}$)n+1-4,
即an=2n+1-4•3n,
则an+1=2n+2-4•3n+1;
∴bn=6an-1+6bn-1=8•3n-3•2n.
综上:an=2n+1-4•3n,bn=6an-1+6bn-1=8•3n-3•2n.
点评 本题考查数列递推式,考查了等比关系的确定,训练了累加法求数列的通项公式,考查计算能力,是中档题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
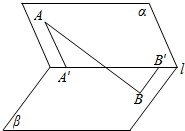 如图,二面角a-l-β为60°,A∈a,B∈β,AA′⊥l交l于A′,BB′⊥l交1于B′,若AA′=2,BB′=1,A′B′=$\sqrt{3}$.
如图,二面角a-l-β为60°,A∈a,B∈β,AA′⊥l交l于A′,BB′⊥l交1于B′,若AA′=2,BB′=1,A′B′=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com