
ЁОЬтФПЁПвЫВ§ЪаФтдк2020ФъЕуОќАТЬхжааФТфГЩКѓЩъАь2022ФъКўББЪЁЪЁдЫЛсЃЌОнСЫНтЃЌФПЧАЮфККЃЌЯхбєЃЌЛЦЪЏЕШЩъАьГЧЪавђЪаУёЕЃаФШќЪТЗбгУГЌжЇЖјзМБИЯрМЬЭЫГіЃЌФГЛњЙЙЮЊЕїВщвЫВ§ЪаЪаУёЖдЩъАьЪЁдЫЛсЕФЬЌЖШЃЌбЁСЫФГаЁЧјЕФ100ЮЛОгУёЕїВщНсЙћЭГМЦШчЯТЃК
жЇГж | ВЛжЇГж | КЯМЦ | |
ФъСфВЛДѓгк50Ыъ | 80 | ||
ФъСфДѓгк50Ыъ | 10 | ||
КЯМЦ | 70 | 100 |
ЃЈ1ЃЉИљОнвбжЊЪ§ОнЃЌАбБэИёЪ§ОнЬюаДЭъећЃЛ
ЃЈ2ЃЉФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТШЯЮЊВЛЭЌФъСфгыжЇГжЩъАьЪЁдЫЛсЮоЙиЃП
ЕФЧАЬсЯТШЯЮЊВЛЭЌФъСфгыжЇГжЩъАьЪЁдЫЛсЮоЙиЃП
ЃЈ3ЃЉвбжЊдкБЛЕїВщЕФФъСфДѓгк50ЫъЕФжЇГжепжага5УћХЎадЃЌЦфжа2ЮЛЪЧХЎНЬЪІЃЌЯжДгет5УћХЎаджаЫцЛњГщШЁ3ШЫЃЌЧѓжСЖрга1ЮЛНЬЪІЕФИХТЪЃЎ
ИНЃК 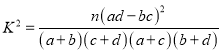 ,
, ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
жЇГж | ВЛжЇГж | КЯМЦ | |
ФъСфВЛДѓгк50Ыъ | 20 | 60 | 80 |
ФъСфДѓгк50Ыъ | 10 | 10 | 20 |
КЯМЦ | 30 | 70 | 100 |
ЃЈ2ЃЉ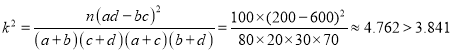 ЃЌ
ЃЌ
ЫљвдФмдкЗИДэЮѓЕФИХТЪВЛГЌЙ§5%ЕФЧАЬсЯТШЯЮЊВЛЭЌФъСфгыжЇГжЩъАьАТдЫЮоЙиЃЛ
(3)МЧ5ШЫЮЊabcde,ЦфжаabБэЪОНЬЪІ,Дг5ШЫШЮвтГщ3ШЫЕФЫљгаЕШПЩФмЪТМўЪЧЃКabc,abd,abe,acd,ace,ade,bcd,bce,bde,cdeЙВ10Иі,ЦфжажСЖр1ЮЛНЬЪІга7ИіЛљБОЪТМўЃКacd,ace,ade,bcd,bce,bde,cde,ЫљвдЫљЧѓИХТЪЪЧ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈжаВЛе§ШЗЕФађКХЮЊ____________ЃЎ
ЂйШєКЏЪ§![]() дк
дк![]() ЩЯЕЅЕїЕнМѕЃЌдђЪЕЪ§
ЩЯЕЅЕїЕнМѕЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЛ
ЃЛ
ЂкКЏЪ§![]() ЪЧХМКЏЪ§ЃЌЕЋВЛЪЧЦцКЏЪ§ЃЛ
ЪЧХМКЏЪ§ЃЌЕЋВЛЪЧЦцКЏЪ§ЃЛ
ЂлвбжЊКЏЪ§![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() ЃЌдђКЏЪ§
ЃЌдђКЏЪ§![]() ЕФЖЈвхгђЪЧ
ЕФЖЈвхгђЪЧ![]() ЃЛ
ЃЛ
ЂмШєКЏЪ§![]() дк
дк![]() ЩЯгазюаЁжЕЃ4ЃЌЃЈ
ЩЯгазюаЁжЕЃ4ЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЮЊЗЧСуГЃЪ§ЃЉЃЌдђКЏЪ§
ЮЊЗЧСуГЃЪ§ЃЉЃЌдђКЏЪ§![]() дк
дк![]() ЩЯгазюДѓжЕ6ЃЎ
ЩЯгазюДѓжЕ6ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЮЊСЫДДНЈШЋЙњЮФУїГЧЪаЃЌУцЯђЩчЛсеаФМжОдИепЃЌЯжДг20ЫъжС50ЫъЕФжОдИепжаАДФъСфЗжзщЃКЕк1зщ![]() ЃЌЕк2зщ
ЃЌЕк2зщ![]() ЃЌЕк3зщ
ЃЌЕк3зщ![]() ЃЌЕк4зщ
ЃЌЕк4зщ![]() ЃЌЕк5зщ
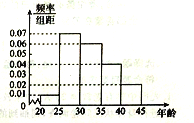
ЃЌЕк5зщ![]() ЃЌЕУЕНЕФЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЌШєгУЗжВуГщбљЕФЗНЗЈДгетаЉжОдИепжаГщШЁ20ШЫВЮМгЁАДДНЈШЋЙњЮФУїГЧЪабщЪеШеЁБЕФЛюЖЏЁЃ
ЃЌЕУЕНЕФЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЌШєгУЗжВуГщбљЕФЗНЗЈДгетаЉжОдИепжаГщШЁ20ШЫВЮМгЁАДДНЈШЋЙњЮФУїГЧЪабщЪеШеЁБЕФЛюЖЏЁЃ
ЃЈ1ЃЉЧѓДгЕк2зщКЭЕк3зщжаГщШЁЕФШЫЪ§ЗжБ№ЪЧЖрЩйЃЛ
ЃЈ2ЃЉШєаЁРюКЭаЁЭѕЖМЪЧ32ЫъЃЌЭЌЪБВЮМгСЫЁАДДНЈШЋЙњЮФУїГЧЪабщЪеШеЁБЕФЛюЖЏЃЌЯжвЊДгЕк3зщГщШЁЕФШЫжаСйЪБГщЕїСНШЫШЅжДааСэвЛШЮЮёЃЌЧѓаЁРюКЭаЁЭѕжСЩйгавЛШЫБЛГщЕїЕФИХТЪЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБШ§РтжљABCЉA1B1C1жаЃЌЁЯBAC=90ЁуЃЌAB=AC=2ЃЌAA1=6ЃЌЕуEЁЂFЗжБ№дкРтBB1ЁЂCC1ЩЯЃЌЧвBE= ![]() BB1 ЃЌ C1F=
BB1 ЃЌ C1F= ![]() CC1 ЃЎ
CC1 ЃЎ 
ЃЈ1ЃЉЧѓЦНУцAEFгыЦНУцABCЫљГЩНЧІСЕФгрЯвжЕЃЛ
ЃЈ2ЃЉШєGЮЊBCЕФжаЕуЃЌA1GгыЦНУцAEFНЛгкHЃЌЧвЩш ![]() =
= ![]() ЃЌЧѓІЫЕФжЕЃЎ
ЃЌЧѓІЫЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЧ![]() БэЪО
БэЪО![]() ЃЌ
ЃЌ![]() жаЕФзюДѓжЕЃЌШч
жаЕФзюДѓжЕЃЌШч![]()
![]() ЃЎвбжЊКЏЪ§
ЃЎвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЩш![]() ЃЌЧѓКЏЪ§
ЃЌЧѓКЏЪ§![]() дк
дк![]() ЩЯСуЕуЕФИіЪ§ЃЛ
ЩЯСуЕуЕФИіЪ§ЃЛ
ЃЈ2ЃЉЪдЬНЬжЪЧЗёДцдкЪЕЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() Жд
Жд![]() КуГЩСЂЃПШєДцдкЃЌЧѓ
КуГЩСЂЃПШєДцдкЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЕЅЕїЕнМѕЃЌдђЪЕЪ§
ЩЯЕЅЕїЕнМѕЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ЁОД№АИЁПC
ЁОНтЮіЁПЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гЩ![]() ЕУ
ЕУ![]() ЃЌ
ЃЌ
ЁрКЏЪ§![]() ЕФЕЅЕїМѕЧјМфЮЊ
ЕФЕЅЕїМѕЧјМфЮЊ![]() ЃЌ
ЃЌ
гжКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЕЅЕїЕнМѕЃЌ
ЩЯЕЅЕїЕнМѕЃЌ
Ёр![]()
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЪЧ
ЕФШЁжЕЗЖЮЇЪЧ![]() ЃЎбЁCЃЎ
ЃЎбЁCЃЎ
ЕуОІЃКвбжЊКЏЪ§дкЧјМфЩЯЕФЕЅЕїадЧѓВЮЪ§ЕФЗНЗЈ
ЃЈ1ЃЉРћгУЕМЪ§ЧѓНтЃЌзЊЛЏЮЊЕМКЏЪ§дкИУЧјМфЩЯДѓгкЕШгкСуЃЈЛђаЁгкЕШгкСуЃЉКуГЩСЂЕФЮЪЬтЧѓНтЃЌвЛАуЭЈЙ§ЗжРыВЮЪ§ЛЏЮЊЧѓКЏЪ§ЕФзюжЕЕФЮЪЬтЃЎ
ЃЈ2ЃЉЯШЧѓГівбжЊКЏЪ§ЕФЕЅЕїЧјМфЃЌШЛКѓНЋЮЪЬтзЊЛЏЮЊЫљИјЕФЧјМфЪЧКЏЪ§ЯргІЕФЕЅЕїЧјМфЕФзгМЏЕФЮЪЬтДІРэЃЎ
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
7
ЁОЬтФПЁПЩш![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЕФЭМЯѓЯђгвЦНвЦ
ЕФЭМЯѓЯђгвЦНвЦ![]() ИіЕЅЮЛГЄЖШКѓгыдЭМЯѓжиКЯЃЌдђ
ИіЕЅЮЛГЄЖШКѓгыдЭМЯѓжиКЯЃЌдђ![]() ЕФзюаЁжЕЪЧЃЈ ЃЉ
ЕФзюаЁжЕЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіКЏЪ§![]() ШчЯТБэЃЌдђfЁВgЃЈxЃЉЁГЕФжЕгђЮЊЃЈ ЃЉ
ШчЯТБэЃЌдђfЁВgЃЈxЃЉЁГЕФжЕгђЮЊЃЈ ЃЉ
x | 1 | 2 | 3 | 4 |
g(x) | 1 | 1 | 3 | 3 |
x | 1 | 2 | 3 | 4 |
f(x) | 4 | 3 | 2 | 1 |
A. {4,2} B. {1,3} C. {1,2,3,4} D. вдЩЯЧщПіЖМгаПЩФм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌНЧAЃЌBЃЌCЫљЖдЕФБпЗжБ№ЮЊaЃЌbЃЌcЃЌЃЈ ![]() aЉsinCЃЉcosB=sinBcosCЃЌb=4
aЉsinCЃЉcosB=sinBcosCЃЌb=4 ![]() ЃЎ
ЃЎ 
ЃЈ1ЃЉЧѓНЧBЕФДѓаЁЃЛ
ЃЈ2ЃЉDЮЊBCБпЩЯвЛЕуЃЌШєAD=2ЃЌSЁїDAC=2 ![]() ЃЌЧѓDCЕФГЄЃЎ
ЃЌЧѓDCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4Љ5ЃКВЛЕШЪНбЁНВ
вбжЊКЏЪ§fЃЈxЃЉ=|xЉ2|Љ|xЉ5|ЃЎ
ЃЈ1ЃЉжЄУїЃКЉ3ЁмfЃЈxЃЉЁм3ЃЛ
ЃЈ2ЃЉЧѓВЛЕШЪНfЃЈxЃЉЁнx2Љ8x+15ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com