
【题目】关于旋转体的体积,有如下的古尔丁(guldin)定理:“平面上一区域D绕区域外一直线(区域D的每个点在直线的同侧,含直线上)旋转一周所得的旋转体的体积,等于D的面积与D的几何中心(也称为重心)所经过的路程的乘积”.利用这一定理,可求得半圆盘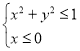 ,绕直线x
,绕直线x![]() 旋转一周所形成的空间图形的体积为_____.
旋转一周所形成的空间图形的体积为_____.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】我国古达数学名著《九章算术-商功》中阐述:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,一为鳖觸,阳马居二,鳖属居一.不易之率也。合两鳖觸三而一,验之以基,其形露矣,”若称为“阳马”的某几何体的三视图如图所示 图中网格纸上小正方形的边长为![]() . 则对该儿何体描述:
. 则对该儿何体描述:

①四个侧面首饰直角三角形
②最长的侧棱长为![]()
③四个侧面中有三个侧面是全等的直角三角形
④外接球的表面积为![]()
其中正确的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》已经政府常务会议审议通过,自2019年12月1日起施行.垃圾分类是对垃圾收集处置传统方式的改革,是对垃圾进行有效处置的一种科学管理方法.所谓垃圾其实都是资源,当你放错了位置时它才是垃圾.某企业在市科研部门的支持下进行研究,把厨余垃圾加工处理为一种可销售的产品.已知该企业每周的加工处理量最少为75吨,最多为100吨.周加工处理成本y(元)与周加工处理量x(吨)之间的函数关系可近似地表示为![]() ,且每加工处理一吨厨余垃圾得到的产品售价为16元.
,且每加工处理一吨厨余垃圾得到的产品售价为16元.
(Ⅰ)该企业每周加工处理量为多少吨时,才能使每吨产品的平均加工处理成本最低?
(Ⅱ)该企业每周能否获利?如果获利,求出利润的最大值;如果不获利,则需要市政府至少补贴多少元才能使该企业不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,下顶点为
,下顶点为![]() ,
,![]() 为椭圆的左、右焦点,过右焦点的直线与椭圆交于
为椭圆的左、右焦点,过右焦点的直线与椭圆交于![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)经过点![]() 的直线与椭圆
的直线与椭圆![]() 交于不同的两点
交于不同的两点![]() (均异于点
(均异于点![]() ),试探求直线
),试探求直线![]() 与
与![]() 的斜率之和是否为定值,证明你的结论.
的斜率之和是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,一个焦点为
,一个焦点为![]() .
.

(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上的任意一点
上的任意一点![]() ,分别作这两条渐近线的平行线与这两条渐近线得到四边形
,分别作这两条渐近线的平行线与这两条渐近线得到四边形![]() ,证明四边形
,证明四边形![]() 的面积是一个定值;
的面积是一个定值;
(3)设直线![]() 与
与![]()
![]() 在第一象限内与渐近线
在第一象限内与渐近线![]() 所围成的三角形
所围成的三角形![]() 绕着
绕着![]() 轴旋转一周所得几何体的体积.
轴旋转一周所得几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=m,点M是棱CD的中点.

(1)求异面直线B1C与AC1所成的角的大小;
(2)是否存在实数m,使得直线AC1与平面BMD1垂直?说明理由;
(3)设P是线段AC1上的一点(不含端点),满足![]() λ,求λ的值,使得三棱锥B1﹣CD1C1与三棱锥B1﹣CD1P的体积相等.
λ,求λ的值,使得三棱锥B1﹣CD1C1与三棱锥B1﹣CD1P的体积相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两直线方程![]() 与
与![]() ,点
,点![]() 在
在![]() 上运动,点
上运动,点![]() 在
在![]() 上运动,且线段
上运动,且线段![]() 的长为定值
的长为定值![]() .
.
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设直线![]() 与点
与点![]() 的轨迹相交于
的轨迹相交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求原点
,求原点![]() 的直线
的直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
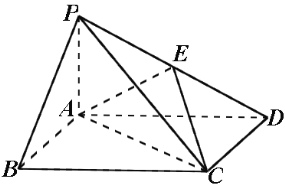
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设PC与平面ABCD所成的角的正弦为![]() ,AP=1,AD=
,AP=1,AD=![]() ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com