
【题目】企业需为员工缴纳社会保险,缴费标准是根据职工本人上一年度月平均工资(单位:元)的![]() 缴纳,
缴纳,
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y(单位:元)与年份序号t的统计如下表:
(1)求出t关于t的线性回归方程![]() ;
;
(2)试预测2019年该员工的月平均工资为多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(注: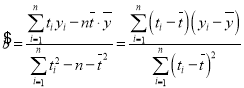 ,
,![]() ,其中
,其中![]() )
)
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.已知随机变量![]() ,若
,若![]() .则
.则![]()
B.已知分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观察值为
的观察值为![]() ,则当
,则当![]() 的值越大时,“
的值越大时,“![]() 与
与![]() 有关”的可信度越小.
有关”的可信度越小.
C.在线性回归模型中,计算其相关指数![]() ,则可以理解为:解析变量对预报变量的贡献率约为
,则可以理解为:解析变量对预报变量的贡献率约为![]()
D.若对于变量![]() 与
与![]() 的
的![]() 组统计数据的线性回归模型中,相关指数
组统计数据的线性回归模型中,相关指数![]() .又知残差平方和为
.又知残差平方和为![]() .那么
.那么![]() .(注意:
.(注意: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“五、校、联、考”四个字,从中任取一个小球,有放回抽取,直到取到“五”“校”二字就停止,用随机模拟的方法估计恰好在第三次停止的概率:利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“五、校、联、考”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下16组随机数,由此可以估计,恰好第三次就停止的概率为______
232 321 230 023 123 021 132 220
231 130 133 231 331 320 120 233
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某件商品的经验表明,该商品每日的销量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为
为常数.已知销售价格为![]() 元/千克时,每日可售出该商品
元/千克时,每日可售出该商品![]() 千克.
千克.
(1)求实数![]() 的值;
的值;
(2)若该商品的成本为![]() 元/千克,试确定销售价格
元/千克,试确定销售价格![]() 的值,使商场每日销售该商品所获得的利润最大,并求出最大值.
的值,使商场每日销售该商品所获得的利润最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的有( )个
(1). 残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高.
(2). 回归直线一定过样本中心![]() 。
。
(3). 两个模型中残差平方和越小的模型拟合的效果越好。
(4) .甲、乙两个模型的![]() 分别约为0.88和0.80,则模型乙的拟合效果更好.
分别约为0.88和0.80,则模型乙的拟合效果更好.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S-ABCD的底面为正方形,SD![]() 底面ABCD如下列结论中不正确的是 。
底面ABCD如下列结论中不正确的是 。
A. AB![]() SA
SA
B. BC//平面SAD
C. BC与SA所成的角等于AD与 SC所成的角
D. SA与平面SBD所成的角等于SC与平面SBD所成的角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com