
【题目】有一个长方形木块,三个侧面积分别为8,12,24,现将其削成一个正四面体模型,则该正四面体模型棱长的最大值为( )
A.2B.![]() C.4D.
C.4D.![]()
科目:高中数学 来源: 题型:
【题目】造纸术、印刷术、指南针、火药被称为中国古代四大发明,此说法最早由英国汉学家艾约瑟提出并为后来许多中国的历史学家所继承,普遍认为这四种发明对中国古代的政治,经济,文化的发展产生了巨大的推动作用.某小学三年级共有学生500名,随机抽查100名学生并提问中国古代四大发明,能说出两种发明的有45人,能说出3种及其以上发明的有32人,据此估计该校三级的500名学生中,对四大发明只能说出一种或一种也说不出的有( )
A.69人B.84人C.108人D.115人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.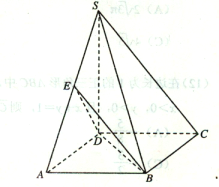
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每个国家对退休年龄都有不一样的规定,从2018年开始我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取100人进行调查,调查情况如下表:
年龄段(单位:岁) |
|
|
|
|
|
|
被调查的人数 |
|
|
|
|
|
|
赞成的人数 |
|
|
|
|
|
|
(1)从赞成“延迟退休”的人中任选1人,此人年龄在![]() 的概率为
的概率为![]() ,求出表格中
,求出表格中![]() 的值;
的值;
(2)在被调查的人中,年龄低于35岁的人可以认为“低龄人”,年龄不低于35岁的人可以认为“非低龄人”,试作出是否赞成“延迟退休”与“低龄与否”的![]() 列联表,并指出有无
列联表,并指出有无![]() 的把握认为是否赞成“延迟退休”与“低龄与否”有关,并说明理由.
的把握认为是否赞成“延迟退休”与“低龄与否”有关,并说明理由.
附:![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为
分别为![]() 的左顶点和上顶点,若
的左顶点和上顶点,若![]() 的中点的纵坐标为
的中点的纵坐标为![]() .
.![]() 分别为
分别为![]() 的左、右焦点.
的左、右焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() ,
,![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以
在以![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走人大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷,某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)求出表格中![]() 的值,并根据表中的数据,判断能否在犯错误的概率不超过
的值,并根据表中的数据,判断能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品对生活无益的人员中随机抽取6人,再从6人中随机抽取2人赠送超市购物券作为答谢,求恰有1人是女性的概率.
参考公式: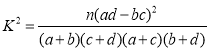 .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大荔县某高中一社团为调查学生学习围棋的情况,随机抽取了![]() 名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于
名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于![]() 分钟的学生称为“围棋迷”.
分钟的学生称为“围棋迷”.
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 |
|
| |
合计 |
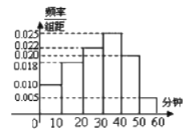
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)现在从参与本次抽样调查的![]() 名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取
名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取![]() 名学生参与围棋知识竞赛,再从
名学生参与围棋知识竞赛,再从![]() 人中任选
人中任选![]() 人参与知识竞赛的赛前保障工作.求选到的
人参与知识竞赛的赛前保障工作.求选到的![]() 人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
附:![]() ,
,
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com