解:(1)
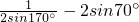
=
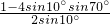
=
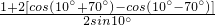
=1;
(2)令tanx=t,∵
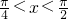
,∴t>1,
∴y=tan2xtan
3x=
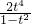
=
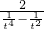
=
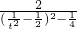
≤
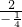
=-8
∴函数y=tan2xtan
3x的最大值为-8;
(3)解:(1)f(x)=sin(2x+θ)+2

×
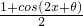
-

=sin(2x+θ)+

cos(2x+θ)=2sin(2x+θ+

);
要使f (x)为偶函数,则必有f(-x)=f(x),
∴2sin(-2x+θ+

)=2sin(2x+θ+

),即-sin[2x-(θ+

)]=sin(2x+θ+

),
整理得:-sin2xcos(θ+

)+cos2xsin(θ+

)=sin2xcos(θ+

)+cos2xsin(θ+

)
即2sin2xcos(θ+

)=0对x∈R恒成立,
∴cos(θ+

)=0,
又0≤θ≤π,则θ=

故答案为:1,-8,A.
分析:(1)通分母,积化和差化简sin70°sin10°,再利用诱导公式,约分得出结果;
(2)利用二倍角公式,转化成关于tanx的函数,将tanx看成整体,最后转化成函数的最值问题解决;
(3)利用二倍角的正弦函数公式、余弦函数公式化简,合并整理后,再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,把函数解析式中的x化为-x,确定出f(-x)的解析式,根据偶函数的性质f(-x)=f(x),列出关系式,利用正弦函数的奇偶性以及两角和与差的正弦函数公式化简,整理后可得cos(θ+

)=0,根据θ的范围,利用特殊角的三角函数值即可求出满足题意θ的度数.
点评:本题考查三角函数知识,考查函数的性质,考查学生解决问题的能力,综合性强.

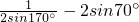 =________;
=________;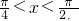 则函数y=tan2xtan3x的最大值为________;
则函数y=tan2xtan3x的最大值为________; )cos(x+
)cos(x+ )+2
)+2 cos2(x+
cos2(x+ )-
)- ,若0≤θ≤π,使函数f(x)为偶函数的θ为________
,若0≤θ≤π,使函数f(x)为偶函数的θ为________ B、
B、 C、
C、 D、
D、 .
.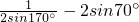 =
=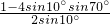 =
=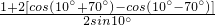 =1;
=1;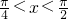 ,∴t>1,
,∴t>1,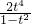 =
=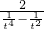 =
=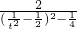 ≤
≤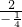 =-8
=-8 ×
×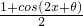 -
-
 cos(2x+θ)=2sin(2x+θ+
cos(2x+θ)=2sin(2x+θ+ );
); )=2sin(2x+θ+
)=2sin(2x+θ+ ),即-sin[2x-(θ+
),即-sin[2x-(θ+ )]=sin(2x+θ+
)]=sin(2x+θ+ ),
), )+cos2xsin(θ+
)+cos2xsin(θ+ )=sin2xcos(θ+
)=sin2xcos(θ+ )+cos2xsin(θ+
)+cos2xsin(θ+ )
) )=0对x∈R恒成立,
)=0对x∈R恒成立, )=0,
)=0,
 )=0,根据θ的范围,利用特殊角的三角函数值即可求出满足题意θ的度数.
)=0,根据θ的范围,利用特殊角的三角函数值即可求出满足题意θ的度数.

 暑假作业安徽少年儿童出版社系列答案
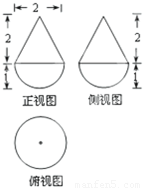
暑假作业安徽少年儿童出版社系列答案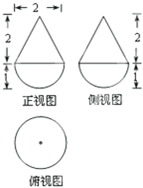 某几何体的三视图如图所示,则该几何体的体积是
某几何体的三视图如图所示,则该几何体的体积是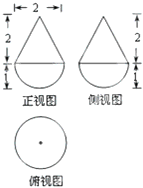 某几何体的三视图如图所示,则该几何体的体积是________;
某几何体的三视图如图所示,则该几何体的体积是________;