设F是抛物线G:x2=4y的焦点.
(Ⅰ)过点P(0,-4)作抛物线G的切线,求切线方程;
(Ⅱ)过抛物线G的焦点F,作两条互相垂直的直线,分别交抛物线于A,C,B,D点,求四边形ABCD面积的最小值.
分析:(I)由题设切线y=kx-4,又x
2=4y联立得x
2-4kx+16=0,由△=0即16k
2-4×16=0,解得k=±2,由此能求出切线方程.
(II)由题意,直线AC斜率存在,由对称性,k>0,AC:y=kx+1,x
2-4kx-4=0,又x
2=4y,x
1+x
2=4kx
1•x
2=-4,所以
|AC|=•=4(1+k
2),同理
|BD|=4[1+(-)2]=,
SABCD=|AC|•|BD|==
8(k2+2+)≥32,由此能导出S
min=32.
解答:解:(I)由题设切线y=kx-4(k显然存在)
又x
2=4y联立得x
2-4kx+16=0
∴△=0即16k
2-4×16=0,解得k=±2
∴切线方程为y=±2x-4
(II)由题意,直线AC斜率存在,又对称性,不妨k>0
∴AC:y=kx+1∴x
2-4kx-4=0
又x
2=4y
∴x
1+x
2=4kx
1•x
2=-4
∴
|AC|=•=4(1+k
2)
同理
|BD|=4[1+(-)2]=∴
SABCD=|AC|•|BD|==
8(k2+2+)≥32当k=1时,“=”成立,∴S
min=32
点评:本题考查切线方程的求法和求四边形ABCD面积的最小值.解题时要认真审题,注意抛物线性质的灵活运用.



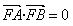 ,延长AF,BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值。
,延长AF,BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值。