
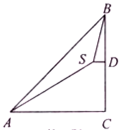
 如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.
如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米. 分析 作出图形,过点S作SE⊥AC于E,SH⊥AB于H,依题意可求得SE在△BDS中利用正弦定理可求BD的长,从而可得山顶高BC.
解答 解:依题意,过S点作SE⊥AC于E,SH⊥AB于H,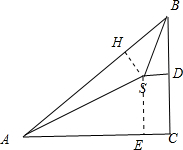 ∵∠SAE=30°,AS=2000米,
∵∠SAE=30°,AS=2000米,
∴CD=SE=AS•sin30°=1000米,
依题意,在Rt△HAS中,∠HAS=45°-30°=15°,
∴HS=AS•sin15°,
在Rt△BHS中,∠HBS=30°,
∴BS=2HS=4000sin15°,
在Rt△BSD中,
BD=BS•sin75°
=4000sin15°•sin75°
=4000sin15°•cos15°
=2000×sin30°
=1000米.
∴BC=BD+CD=1000+1000=2000米;
故答案为:2000.
点评 本题考查正弦定理的应用,考查作图与计算的能力,关键是将实际问题转化为数学问题中的解三角形的问题解答;属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | f2(x)<f(x2)<f(x) | B. | f(x2)<f2(x)<f(x) | C. | f(x)<f(x2)<f2(x) | D. | f(x2)<f(x)<f2(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
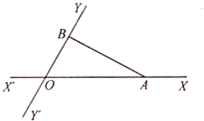 如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.
如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=3-x | B. | y=x2-3x | C. | $f(x)={(\frac{1}{2})^x}$ | D. | f(x)=|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 参加数学第二课堂活动 | p | ||
| 未参加数学第二课堂活动 | q | 100 | |
| 总计 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com