
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上的动点,给出下列说法:①
上的动点,给出下列说法:①![]() 与
与![]() 所成的最大角为
所成的最大角为![]() ;②
;②![]() 的最小值为
的最小值为![]() ;③
;③![]() 与
与![]() 垂直;④若
垂直;④若![]() 为
为![]() 的中点,则四面体
的中点,则四面体![]() 的体积为
的体积为![]() .其中正确的个数有( )
.其中正确的个数有( )

A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36B.72C.108D.144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到直线
到直线![]() 的距离比到定点
的距离比到定点![]() 的距离大1.
的距离大1.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)若![]() 为直线
为直线![]() 上一动点,过点
上一动点,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() ,
,![]() ,切点为
,切点为![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
①求证:![]() 轴;
轴;
②直线![]() 是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入![]() ,则输出的结果是( )
,则输出的结果是( )
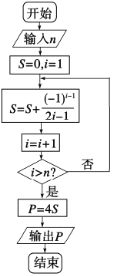
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.若圆C上存在点M,使MA=2MO,则圆心C的横坐标a的取值范围是( )
A.![]() B.[0,1]
B.[0,1]
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2018年1月至12月石油进口量统计图(其中同比是今年第![]() 个月与去年第
个月与去年第![]() 个月之比),则下列说法错误的是( )
个月之比),则下列说法错误的是( )

A.2018年下半年我国原油进口总量高于2018年上半年
B.2018年12个月中我国原油月最高进口量比月最低进口量高1152万吨
C.2018年我国原油进口总量高于2017年我国原油进口总量
D.2018年1月—5月各月与2017年同期相比较,我国原油进口量有增有减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市抽查了100天该超市的日纯利润数据,并将日纯利润数据分成以下几组(单位:万元):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计结果如下表所示:
,统计结果如下表所示:
组别 |
|
|
|
|
|
|
频数 | 5 | 20 | 30 | 30 | 10 | 5 |
以上述样本分布的频率估计总体分布的概率,解决下列问题:
(1)从该大型超市近几年的销售记录中抽出5天,求其中日纯利润在区间![]() 内的天数不少于2的概率;
内的天数不少于2的概率;
(2)该超市经理由频数分布表可以认为,该大型超市每天的纯利润![]() 服从正态分布
服从正态分布![]() ,其中,
,其中,![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值).
(每组数据取区间的中点值).
①试利用该正态分布,估计该大型超市1000天内日纯利润在区间![]() 内的天数(精确到个位);
内的天数(精确到个位);
②该大型超市负责人根据每日的纯利润给超市员工制定了两种不同的奖励方案:
方案一:直接发放奖金,日纯利润低于![]() 时每名员工发放奖金70元,日纯利润不低于
时每名员工发放奖金70元,日纯利润不低于![]() 时每名员工发放奖金90元;
时每名员工发放奖金90元;
方案二:利用抽奖的方式获得奖金,其中日纯利润不低于![]() 时每位员工均有两次抽奖机会,日纯利润低于
时每位员工均有两次抽奖机会,日纯利润低于![]() 时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
时每位员工只有一次抽奖机会;每次抽奖的奖金及对应的概率分别为
金额 | 50元 | 100元 |
概率 |
|
|
小张恰好为该大型超市的一名员工,则从数学期望的角度看,小张选择哪种奖励方案更有利?
参考数据:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修 4-4]参数方程与极坐标系
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: ![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,取相同的单位长度建立极坐标系.已知直线
轴正半轴为极轴,取相同的单位长度建立极坐标系.已知直线 ![]() :
: ![]() .
.
(Ⅰ)试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
[选修 4-5]不等式选讲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奇函数f(x)在R上存在导数![]() ,当x<0时,
,当x<0时,![]()
![]() f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(0,1)
C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com