
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.若直线
两点.若直线![]() 上存在点
上存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形,求
是平行四边形,求![]() 的值.
的值.
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型娱乐场有两种型号的水上摩托,管理人员为了了解水上摩托的使用及给娱乐城带来的经济收入情况,对该场所最近6年水上摩托的使用情况进行了统计,得到相关数据如表:
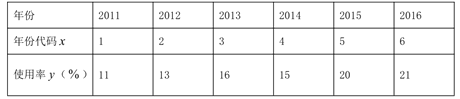
(1)请根据以上数据,用最小二乘法求水上摩托使用率![]() 关于年份代码
关于年份代码![]() 的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
(2)随着生活水平的提高,外出旅游的老百姓越来越多,该娱乐场根据自身的发展需要,准备重新购进一批水上摩托,其型号主要是目前使用的Ⅰ型、Ⅱ型两种,每辆价格分别为1万元、1.2万元.根据以往经验,每辆水上摩托的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:
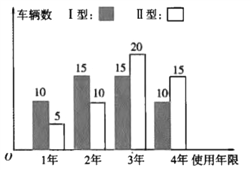
已知每辆水上摩托从购入到淘汰平均年收益是0.8万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润=收益-购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?
附:回归直线方程为![]() ,其中
,其中 ,
, ![]() .参考数据
.参考数据![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论错误的是( )
A. 命题“若x2-3x-4=0,则x=4”的逆否命题是“若x≠4,则x2-3x-4≠0”
B. 命题“若m>0,则方程x2+x-m=0有实根”的逆命题为真命题
C. “x=4”是“x2-3x-4=0”的充分条件
D. 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-e-x(x∈R,且e为自然对数的底数).
(1)判断函数f(x)的单调性与奇偶性;
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x∈R都成立?若存在,求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知曲线![]() ,曲线
,曲线![]() 的左右焦点是
的左右焦点是![]() ,
, ![]() ,且
,且![]() 就是
就是![]() 的焦点,点
的焦点,点![]() 是
是![]() 与
与![]() 的在第一象限内的公共点且
的在第一象限内的公共点且![]() ,过
,过![]() 的直线
的直线![]() 分别与曲线
分别与曲线![]() 、
、![]() 交于点
交于点![]() 和
和![]() .
.

(Ⅰ)求点![]() 的坐标及
的坐标及![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 面积分别是
面积分别是![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com