
【题目】设a为实数,函数f(x)=x|x﹣a|.
(1)讨论f(x)的奇偶性;
(2)当0≤x≤1时,求f(x)的最大值.
【答案】
(1)解:由题意可知函数f(x)的定义域为R.
当a=0时f(x)=x|x﹣a|=x|x|,为奇函数.
当a≠0时,f(x)=x|x﹣a|,
f(1)=|1﹣a|,f(﹣1)=﹣|1+a|,
f(﹣x)≠f(x)且f(﹣x)≠﹣f(x),
∴此时函数f(x)为非奇非偶函数
(2)解:若a≤0,则函数f(x)=x|x﹣a|在0≤x≤1上为增函数,
∴函数f(x)的最大值为f(1)=|1﹣a|=1﹣a,
若a>0,由题意可得f(x)= 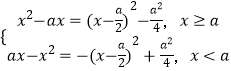 ,
,
由于a>0且0≤x≤1,结合函数f(x)的图象可知,
由 ![]() ,
,
当 ![]() ,即a≥2时,f(x)在[0,1]上单调递增,
,即a≥2时,f(x)在[0,1]上单调递增,
∴f(x)的最大值为f(1)=a﹣1;
当 ![]() ,
,
即 ![]() 时,f(x)在[0,
时,f(x)在[0, ![]() ]上递增,在[
]上递增,在[ ![]() ,a]上递减,
,a]上递减,
∴f(x)的最大值为f( ![]() )=
)= ![]() ;
;
当 ![]() ,即
,即 ![]() 时,
时,
f(x)在[0, ![]() ]上递增,在[
]上递增,在[ ![]() ,a]上递减,在[a,1]上递增,
,a]上递减,在[a,1]上递增,
∴f(x)的最大值为f(1)=1﹣a
【解析】(1)先得出函数f(x)的定义域为R,对a分类讨论,结合函数的奇偶性的定义可得结果,(2)当a≤0时,f(x)=x|x﹣a|在0≤x≤1上为增函数,此时最大值为f(x)=1-a,当a>0时,对二次函数进行定区间讨论得出最大值.
【考点精析】通过灵活运用函数的最值及其几何意义,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值即可以解答此题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是C: ![]() +
+ ![]() =1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为 ![]() ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围是( )
的取值范围是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集为R,集合A={x|y=lgx+ ![]() },B={x|
},B={x| ![]() <2x﹣a≤8}.
<2x﹣a≤8}.
(1)当a=0时,求(RA)∩B;
(2)若A∪B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】建造一个容积为240m3 , 深为5m的长方体无盖蓄水池,池壁的造价为180元/m2 , 池底的造价为350元/m2 , 如何设计水池的长与宽,才能使水池的总造价为42000元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2ax+2+b,(a≠0),若f(x)在区间[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)﹣mx在[2,4]上为单调函数,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对实数a和b,定义运算“”:ab= ![]() ,设函数f(x)=(x2﹣2)(x﹣x2),x∈R,若函数y=f(x)+c的图象与x轴恰有两个公共点,则实数c的取值范围是 .
,设函数f(x)=(x2﹣2)(x﹣x2),x∈R,若函数y=f(x)+c的图象与x轴恰有两个公共点,则实数c的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com