
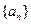 和
和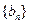 满足
满足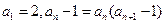 ,
,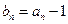 ,数列
,数列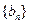 的前
的前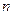 和为
和为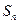 .
.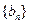 的通项公式;
的通项公式; (2)设
(2)设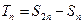 ,求证:
,求证: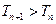 ;
;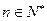 有
有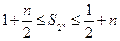 成立.
成立.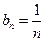
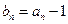 得
得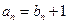 代入
代入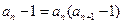 得
得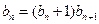
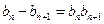 ,-----------------------------------------------------1分
,-----------------------------------------------------1分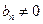 否则
否则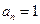 ,与
,与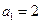 矛盾
矛盾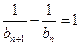 , ----------------------------------------------------------3分
, ----------------------------------------------------------3分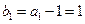
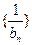 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列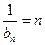 ,即
,即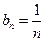 .---------------------------------------------------------------4分
.---------------------------------------------------------------4分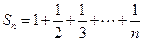
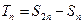 =
=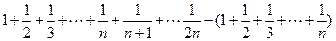
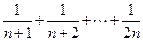 ---------------------------------------------------------6分
---------------------------------------------------------6分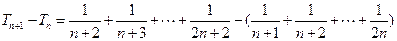
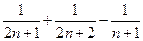 =
=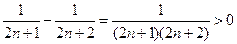
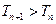 .--------------------------------------------------------------------------8分
.--------------------------------------------------------------------------8分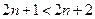 ∴
∴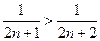
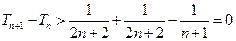
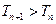 .----------------------------------------------------------------------------8分
.----------------------------------------------------------------------------8分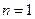 时
时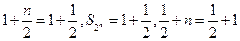 ,不等式成立;-----------9分
,不等式成立;-----------9分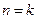 (
(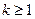 ,
,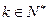 )时,不等式成立,即
)时,不等式成立,即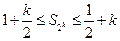 ,那么当
,那么当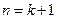 时
时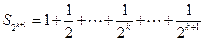
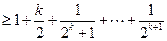
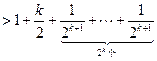
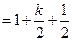
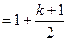 ----------------------------------------------------------------------12分
----------------------------------------------------------------------12分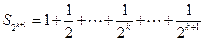
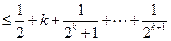
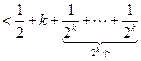
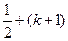
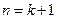 时,不等式成立
时,不等式成立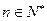 ,不等式成立.--------------------------------------------------------
,不等式成立.--------------------------------------------------------

 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源:不详 题型:解答题
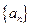 的前
的前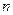 项和是
项和是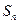 ,且
,且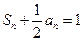 .
.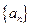 的通项公式;
的通项公式;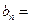
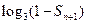 ,求适合方程
,求适合方程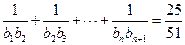 的
的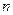 的值.
的值.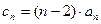 ,是否存在实数M,使得对一切
,是否存在实数M,使得对一切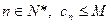 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
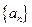 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表: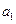
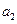
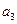


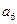



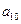
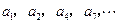 构成的数列为
构成的数列为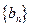 ,
,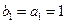 .
.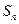 为数列
为数列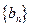 的前
的前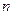 项和,且满足
项和,且满足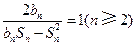 .
.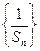 成等差数列,并求数列
成等差数列,并求数列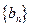 的通项公式;
的通项公式;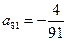 时,求上表中第
时,求上表中第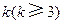 行所有项的和.
行所有项的和.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com