
设![]() ,等差数列
,等差数列![]() 中
中![]() ,
,![]() ,记
,记![]() =
=![]() ,令
,令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(Ⅰ)求![]() 的通项公式和
的通项公式和![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)是否存在正整数![]() ,且
,且![]() ,使得
,使得![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
科目:高中数学 来源: 题型:
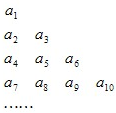 将数列{an}中的所有项按每一行比上一行多一项的规则排成如数表:
将数列{an}中的所有项按每一行比上一行多一项的规则排成如数表:| 2bn | ||
bnSn-
|
| 1 |
| Sn |
| 4 |
| 91 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年聊城市四模理) (14分) 在直角坐标平面上有一点列![]() 位于直线
位于直线![]() 上,且Pn的横坐标构成以
上,且Pn的横坐标构成以![]() 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,…,Cn,…中的每一条的对称轴都垂直于x轴,第n条抛物线Cn的顶点为Pn,且经过点Dn(0,n2+1)![]() . 记与抛物线Cn相切于点Dn的直线的斜率为kn,求证:
. 记与抛物线Cn相切于点Dn的直线的斜率为kn,求证:![]() ;
;
(3)设![]() ,等差数列{an}的任意一项
,等差数列{an}的任意一项![]() ,其中a1是S∩T中的最大数,且-256<a10<-125,求数列{an}通项公式.
,其中a1是S∩T中的最大数,且-256<a10<-125,求数列{an}通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,给出了一个三角形数阵,已知每一列的数成等差数列,从第3行起,每一行的数成等比数列,每一行的公比都相等.记第![]() 行第
行第![]() 列的数为
列的数为![]() (
(![]() ∈N*).
∈N*).
(1)试写出![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() ;
;
(2)设数阵中第n行的所有数之和为An, 求An
查看答案和解析>>
科目:高中数学 来源: 题型:
a11,a12,……a18
a21,a22,……a28
……………………
64个正数排成8行8列, 如下所示: a81,a82,……a88
在符合![]() 中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且
中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且![]() ,
,![]() ,
,![]() 。
。
⑴若![]() ,求
,求![]() 和
和![]() 的值。
的值。
⑵记第n行各项之和为An(1≤n≤8),数列{an}、{bn}、{cn}满足![]() ,联
,联![]() (m为非零常数),
(m为非零常数),![]() ,且
,且![]() ,求
,求![]() 的取值范围。
的取值范围。
⑶对⑵中的![]() ,记
,记![]() ,设
,设![]() ,求数列
,求数列![]() 中最大项的项数。
中最大项的项数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com