【题目】若冬季昼夜温差x（单位：
）与某新品种反季节大豆的发芽数量y（单位：颗）具有线性相关关系，根据一组样本数据
，用最小二乘法近似得到回归直线方程为
，则下列结论中不正确的是（ ）
A.y与x具有正相关关系
B.回归直线过点
C.若冬季昼夜温差增加
，则该新品种反季节大豆的发芽数约增加2.5颗
D.若冬季昼夜温差的大小为
，则该新品种反季节大豆的发芽数一定是22颗
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝ax+lnx（a∈R），g（x）＝x2emx（m∈R，e为自然对数的底数）．
（1）讨论函数f（x）的单调性及最值；
（2）若a＞0，且对x1，x2∈[0，2]，f（x1+1）≥g（x2）+a﹣1恒成立，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“大众创业，万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据
，如表所示：
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 | q | 84 | 83 | 80 | 75 | 68 |
已知
，
.
（Ⅰ）求出
的值；
（Ⅱ）已知变量
，
具有线性相关关系，求产品销量（件）关于试销单价（元）的线性回归方程
；
（Ⅲ）用
表示用（Ⅱ）中所求的线性回归方程得到的与
对应的产品销量的估计值.当销售数据
对应的残差的绝对值
时，则将销售数据称为一个“好数据”.现从6个销售数据中任取2个，求“好数据”至少有一个的概率.
（参考公式：线性回归方程中
，
的最小二乘估计分别为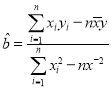
，
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的一个焦点为
，离心率为
.
为椭圆
的左顶点，
为椭圆上异于的两个动点，直线
与直线
分别交于
两点.
（I）求椭圆的方程；
（II）若
与
的面积之比为
，求
的坐标；
（III）设直线
与
轴交于点
，若
三点共线，求证：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在全国第五个“扶贫日”到来之前，某省开展“精准扶贫，携手同行”的主题活动，某贫困县调查基层干部走访贫困户数量．甲镇有基层干部60人，乙镇有基层干部60人，丙镇有基层干部80人，每人都走访了若干贫困户，按照分层抽样，从甲、乙、丙三镇共选20名基层干部，统计他们走访贫困户的数量，并将走访数量分成
，
，
，
，
5组，绘制成如图所示的频率分布直方图．
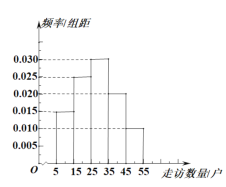
（1）求这20人中有多少人来自丙镇，并估计甲、乙、丙三镇的基层干部走访贫困户户数的中位数（精确到整数位）；
（2）如果把走访贫困户达到或超过35户视为工作出色，求选出的20名基层干部中工作出色的人数，并从中选2人做交流发言，求这2人中至少有一人走访的贫困户在的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
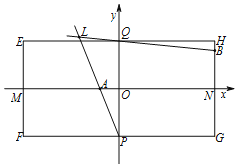
【题目】如图，在平面直角坐标系xOy中，已知点O（0，0），M（-4，0），N（4，0），P（0，-2），Q（0，2），H（4，2）．线段OM上的动点A满足
；线段HN上的动点B满足
．直线PA与直线QB交于点L，设直线PA的斜率记为k，直线QB的斜率记为k'，则kk'的值为______；当λ变化时，动点L一定在______（填“圆、椭圆、双曲线、抛物线”之中的一个）上．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
