
【题目】设函数f(x)=x(x﹣1)2 , x>0.
(1)求f(x)的极值;
(2)设0<a≤1,记f(x)在(0,a]上的最大值为F(a),求函数 ![]() 的最小值;
的最小值;
(3)设函数g(x)=lnx﹣2x2+4x+t(t为常数),若使g(x)≤x+m≤f(x)在(0,+∞)上恒成立的实数m有且只有一个,求实数m和t的值.
【答案】
(1)解:f′(x)=(x﹣1)2+2x(x﹣1)=3x2﹣4x+1=(3x﹣1)(x﹣1),x>0.令f′(x)=0,得x= ![]() 或x=1,f(x),f′(x)随x的变化情况如下表
或x=1,f(x),f′(x)随x的变化情况如下表 
∴当x= ![]() 时,有极大值f(
时,有极大值f( ![]() )=
)= ![]() ,当x=1时,有极小值f(1)=0
,当x=1时,有极小值f(1)=0
(2)解:由(1)知:f(x)在(0, ![]() ],[1,+∞)上是增函数,在[
],[1,+∞)上是增函数,在[ ![]() ,1]上是减函数,
,1]上是减函数,
①0<a≤ ![]() 时,F(a)=a(a﹣1)2,G(a)=(a﹣1)2≥
时,F(a)=a(a﹣1)2,G(a)=(a﹣1)2≥ ![]()
特别的,当a= ![]() 时,有G(a)=
时,有G(a)= ![]() ,
,
②当 ![]() <a≤1时,F(a)=f(
<a≤1时,F(a)=f( ![]() )=
)= ![]() ,G(a)=
,G(a)= ![]() ≥
≥ ![]()
特别的,当a=1时,有G(a)= ![]() ,
,
由①②知,当0<a≤1时,函数 ![]() 的最小值为
的最小值为 ![]()
(3)解:由已知得h1(x)=x+m﹣g(x)=2x2﹣3x﹣lnx+m﹣t≥0在(0,+∞)上恒成立,
∵ ![]() ,
,
∴x∈(0,1)时,h′1(x)<0,x∈(1,+∞)时,h1(x)>0
∴x=1时,h′1(x)取极小值,也是最小值,
∴当h1(1)=m﹣t﹣1≥0,m≥t+1时,h1(x)≥0在(0,+∞)上恒成立,
同样,h2(x)=f(x)﹣x﹣m=x3﹣2x2﹣m≥0在(0,+∞)上恒成立,
∵h′2(x)=3x(x﹣ ![]() ),
),
∴x∈(0, ![]() )时,h′2(x)<0,x∈(
)时,h′2(x)<0,x∈( ![]() ,+∞),h′2(x)>0,
,+∞),h′2(x)>0,
∴x= ![]() 时,h2(x)取极小值,也是最小值,
时,h2(x)取极小值,也是最小值,
∴ ![]() =﹣
=﹣ ![]() ﹣m≥0,m≤﹣
﹣m≥0,m≤﹣ ![]() 时,h2(x)≥0在(0,+∞)上恒成立,
时,h2(x)≥0在(0,+∞)上恒成立,
∴t+1≤m≤﹣ ![]() ,
,
∵实数m有且只有一个,∴m=﹣ ![]() ,t=
,t= ![]()
【解析】(1)求导,令f′(x)=0得x= ![]() 或x=1,令f′(x)>0,令f′(x)<0得f(x)的单调性,确定函数f(x)的极值.(2)由(1)知f(x)的单调性,以极值点为界,把a分成两类讨论,在两类分别求出F(a),求G(a),求G(a)最小值,两个最小值最小者,即为所求.(3)把连等式分成两个不等式x+m﹣g(x)≥0和f(x)﹣x﹣m≥0在(0,+∞)上恒成立的问题,把不等式的左边看作一个函数,利用导数求最小值,两个范围求交集再由实数m有且只有一个,可求m,进而求t.
或x=1,令f′(x)>0,令f′(x)<0得f(x)的单调性,确定函数f(x)的极值.(2)由(1)知f(x)的单调性,以极值点为界,把a分成两类讨论,在两类分别求出F(a),求G(a),求G(a)最小值,两个最小值最小者,即为所求.(3)把连等式分成两个不等式x+m﹣g(x)≥0和f(x)﹣x﹣m≥0在(0,+∞)上恒成立的问题,把不等式的左边看作一个函数,利用导数求最小值,两个范围求交集再由实数m有且只有一个,可求m,进而求t.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,b1=1,且b2S2=64,b3S3=960.
(1)求an与bn;
(2)求![]()
【答案】(1)an=2n+1,bn=8n-1.(2)![]()
【解析】
(1)设{an}的公差为d,{bn}的公比为q,由题设条件建立方程组,解方程组得到d和q的值,从而求出an与bn;(2)由Sn=n(n+2),知![]() ,由此可求出
,由此可求出![]() 的值.
的值.
(1)设{an}的公差为d,{bn}的公比为q,则d为正数,
an=3+(n-1)d,bn=qn-1,
依题意有![]() ,
,
解得![]() 或
或 (舍去).
(舍去).
故an=3+2(n-1)=2n+1,bn=8n-1.
(2)Sn=3+5+…+(2n+1)=n(n+2).
所以![]() +
+![]() +…+
+…+![]() =
=![]() +
+![]() +
+![]() +…+
+…+![]()
=![]() (1-
(1-![]() +
+![]() -
-![]() +
+![]() -
-![]() +…+
+…+![]() -
-![]() )
)
=![]() (1+
(1+![]() -
-![]() -
-![]() )
)
=![]() -
-![]() .
.
【点睛】
这个题目考查的是数列通项公式的求法及数列求和的常用方法;数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等。
做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等。
【题型】解答题
【结束】
21
【题目】已知函数f(x)满足f(x+y)=f(x)·f(y),且f(1)=![]() .
.
(1)当n∈N+,求f(n)的表达式;
(2)设an=nf(n),n∈N+,求证:a1+a2+…+an<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)(x∈R)d的导函数为f′(x),若f(x)﹣f(﹣x)=2x3 , 且当x≥0时,f′(x)>3x2 , 则不等式f(x)﹣f(x﹣1)>3x2﹣3x+1的解集是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
, ![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 交椭圆
交椭圆![]() 于另一个点
于另一个点![]() ,求
,求![]() 面积取得最大值时直线
面积取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2. 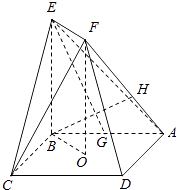
(1)求证:EG∥平面ADF;
(2)求二面角O﹣EF﹣C的正弦值;
(3)设H为线段AF上的点,且AH= ![]() HF,求直线BH和平面CEF所成角的正弦值.
HF,求直线BH和平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】怀化某中学对高三学生进行体质测试,已知高三某个班有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm)
男生成绩在195cm以上(包含195cm)定义为“合格”,成绩在195cm以下(不包含195cm)定义为“不合格”,女生成绩在185cm以上(包含185cm)定义为“合格”,成绩在185cm以下(不包含185cm)定义为“不合格”.
(1)求女生立定跳远成绩的中位数;
(2)若在男生中按成绩合格与否进行分层抽样,抽取6人,求抽取成绩为“合格”的学生人数;
(3)若从(2)中抽取的6名学生中任意选取4个人参加复试,求这4人中至少3人合格的概率. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)从6名同学中选4名同学组成一个代表队,参加4×400米接力比赛,问有多少种参赛方案?
(2)从6名同学中选4名同学参加场外啦啦队,问有多少种选法?
(3) 4名同学每人可从跳高、跳远、短跑三个项目中,任选一项参加比赛,问有多少种参赛方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com