
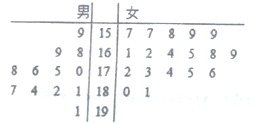
【题目】双流中学校运动会招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位: ![]() ),身高在175
),身高在175![]() 以上(包括175
以上(包括175![]() )定义为“高个子”,身高在175
)定义为“高个子”,身高在175![]() 以 下(不包括175
以 下(不包括175![]() )定义为“非高个子”.
)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率?
(2)若从身高180![]() 以上(包括180
以上(包括180![]() )的志愿者中选出男、女各一人,求这两人身高相差5
)的志愿者中选出男、女各一人,求这两人身高相差5![]() 以上的概率.
以上的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)求出用分层抽样的方法抽取的“个子高”与“非个子高”的人数,列举出抽出两人的所有情况和符合条件的所有情况情况再根据古典概型概率公式可得结果;(2)先计列举出从身高![]() 以上(包括
以上(包括![]() )的志愿者中选出男、女各一人的事件总数,再列举出这2人身高相差
)的志愿者中选出男、女各一人的事件总数,再列举出这2人身高相差![]() 以上的事件数,代入古典概率公式,可得答案.
以上的事件数,代入古典概率公式,可得答案.
试题解析:(1)根据茎叶图,有“高个子”12人,“非高个子”18人,
用分层抽样的方法,每个人被抽中的概率是![]() ,
,
所以选中的“高个子”有![]() 人,“非高个子”有
人,“非高个子”有![]() 人.
人.
“高个子”用![]() 和
和![]() 表示,“非高个子”用
表示,“非高个子”用![]() 表示,则抽出两人的情况有:
表示,则抽出两人的情况有: ![]() 共10种,至少有一个“高个子”被选中有
共10种,至少有一个“高个子”被选中有![]() ,共7种,用事件
,共7种,用事件![]() 表示“至少有一名“高个子”被选中”,则
表示“至少有一名“高个子”被选中”,则![]() .
.
(2抽出的两人身高用(男身高,女身高)表示,则有![]()
![]() ,共10种情况,身高相差5
,共10种情况,身高相差5![]() 以上的:
以上的: ![]() ,共4种情况,用事件
,共4种情况,用事件![]() 表示“身高相差5
表示“身高相差5![]() 以上”,则
以上”,则![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() .
.
(1)写出曲线![]() ,
, ![]() 的普通方程;
的普通方程;
(2)过曲线![]() 的右焦点
的右焦点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() ,该直线与曲线
,该直线与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x∈R)
(x∈R)
(1)用定义证明f(x)是增函数;
(2)若g(x)=f(x)﹣a是奇函数,求g(x)在(﹣∞,a]上的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 ![]() .类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
.类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 . 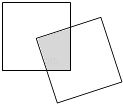
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某学校简单随机抽样方法抽取了100名同学,对其日均课外阅读时间:(单位:分钟)进行调查,结果如下:

若将日均课外阅读时间不低于60分钟的学生称为“读书迷”
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
①求抽取的4为同学中有男同学又有女同学的概率;
②记抽取的“读书迷”中男生人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2+log3x,x∈[1,9],g(x)=[f(x)]2+f(x2),
(1)求g(x)的定义域;
(2)求g(x)的最大值以及g(x)取最大值时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com