
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,焦距为2c,且c,
,焦距为2c,且c, ![]() ,2成等比数列.
,2成等比数列.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)点B坐标为(0, ![]() ),问是否存在过点B的直线l交椭圆C于M,N两点,且满足
),问是否存在过点B的直线l交椭圆C于M,N两点,且满足![]() (O为坐标原点)?若存在,求出此时直线l的方程;若不存在,请说明理由.
(O为坐标原点)?若存在,求出此时直线l的方程;若不存在,请说明理由.
【答案】(Ⅰ) ![]() +y2=1(Ⅱ)y=
+y2=1(Ⅱ)y=![]() x+
x+![]() 或y=-
或y=-![]() x+
x+![]() .
.
【解析】试题分析:(Ⅰ)根据题意可以知道: (![]() )2=2·c ,椭圆的离心率可得a=
)2=2·c ,椭圆的离心率可得a=![]() ,即可求得a和b的值,即可求得椭圆方程;
,即可求得a和b的值,即可求得椭圆方程;
(Ⅱ)设直线MN的方程,代入椭圆方程,由韦达定理及向量数量积的坐标运算,即可求得k的值,直线l的方程.
试题解析:(Ⅰ)( ![]() )2=2·c,解得c=1.
)2=2·c,解得c=1.
又e′=![]() =
=![]() ,及a2=b2+c2,解得a=
,及a2=b2+c2,解得a=![]() ,b=1.
,b=1.
所以椭圆C的标准方程为![]() +y2=1.
+y2=1.
(Ⅱ)若直线l过点B(0, ![]() ).
).
当直线l的斜率不存在时,显然不符合题意;
故直线l的斜率存在,设为k,则直线l的方程为y-![]() =kx,即y=kx+
=kx,即y=kx+![]() .
.
联立方程组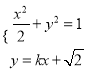 消去y,得(1+2k2)x2+4
消去y,得(1+2k2)x2+4![]() kx+2=0.
kx+2=0.
显然Δ=(4![]() k)2-4(1+2k2)×2>0,
k)2-4(1+2k2)×2>0,
解得k>![]() 或k<-
或k<-![]() .(*)
.(*)
设点M(x1,y1),N(x2,y2),
则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
由![]() ,得
,得![]() =0,则x1x2+y1y2=0.
=0,则x1x2+y1y2=0.
即![]() +(kx1+
+(kx1+![]() )(kx2+
)(kx2+![]() )=0,得
)=0,得![]() +k2x1x2+
+k2x1x2+![]() k(x1+x2)+2=0,
k(x1+x2)+2=0,
得![]() +k2·
+k2·![]() +
+![]() k
k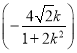 +2=0,
+2=0,
化简得![]() =0,解得k=±
=0,解得k=±![]() .符合(*)式,
.符合(*)式,
此时直线l的方程为y=![]() x+
x+![]() 或y=-
或y=-![]() x+
x+![]() .
.
故存在过点B的直线l交椭圆C于M,N两点,且满足![]() ,
,
此时直线l的方程为y=![]() x+
x+![]() 或y=-
或y=-![]() x+
x+![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.
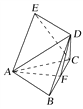
(1)试确定F的位置;
(2)求三棱锥A-CDF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点.

求证:(1)E、C、D1、F四点共面;
(2)CE、D1F、DA三线共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的准线方程为x=-1,过定点M(m,0)(m>0)作斜率为k的直线l交抛物线C于A,B两点,E是M点关于坐标原点O的对称点,若直线AE和BE的斜率分别为k1,k2,则k1+k2=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
平面直角坐标系xOy中,射线l:y=![]() x(x≥0),曲线C1的参数方程为
x(x≥0),曲线C1的参数方程为![]() (α为参数),曲线C2的方程为x2+(y-2)2=4;以原点为极点,x轴的非负半轴为极轴建立极坐标系. 曲线C3的极坐标方程为ρ=8sin θ.
(α为参数),曲线C2的方程为x2+(y-2)2=4;以原点为极点,x轴的非负半轴为极轴建立极坐标系. 曲线C3的极坐标方程为ρ=8sin θ.
(Ⅰ)写出射线l的极坐标方程以及曲线C1的普通方程;
(Ⅱ)已知射线l与C2交于O,M,与C3交于O,N,求|MN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=(sin x,mcos x),b=(3,-1).
(1)若a∥b,且m=1,求2sin2x-3cos2x的值;
(2)若函数f(x)=a·b的图象关于直线![]() 对称,求函数f(2x)在
对称,求函数f(2x)在![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn,且3an+Sn=4(n∈N*).
(1)证明:{an}是等比数列;
(2)在an和an+1之间插入n个数,使这n+2个数成等差数列.记插入的n个数的和为Tn,求Tn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线M的参数方程为![]() (θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+
(θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+![]() )=
)=![]() t(其中t为常数).
t(其中t为常数).
(Ⅰ)若曲线N与曲线M只有一个公共点,求t的值;
(Ⅱ)当t=-1时,求曲线M上的点与曲线N上的点的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856266)[选修4-5:不等式选讲]
设函数f(x)=|2x-1|-|x+2|.
(Ⅰ)解不等式f(x)>0;
(Ⅱ)若x0∈R,使得f![]() +2m2<4m,求实数m的取值范围.
+2m2<4m,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com