
(本题满分10分)已知函数 .
.
(I)讨论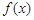 的单调性;
的单调性;
(II)设 ,证明:当
,证明:当 时,
时, ;
;
(III)若函数 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
证明: (x0)<0.
(x0)<0.
(1)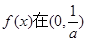 单调增加,在
单调增加,在 单调减少;(2)当
单调减少;(2)当 ,
, (3)见解析.
(3)见解析.
【解析】第一问利用导数求解得到。
(I)

(i)若 单调增加.
单调增加.
(ii)若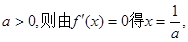 且当
且当
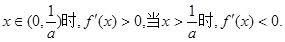
所以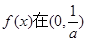 单调增加,在
单调增加,在 单调减少.
单调减少.
第二问中,构造函数设函数 则
则

结合导数得到单调性判定进而求解。
第三问中,由(I)可得,当 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,
故 ,从而
,从而 的最大值为
的最大值为
解:(I)

(i)若 单调增加.
单调增加.
(ii)若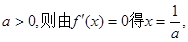 且当
且当

所以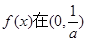 单调增加,在
单调增加,在 单调减少. ………………3分
单调减少. ………………3分
(II)设函数 则
则

当 .
.
故当 ,
, ………………6分
………………6分
(III)由(I)可得,当 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,
故 ,从而
,从而 的最大值为
的最大值为
不妨设

由(II)得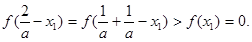 从而
从而
由(I)知,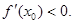 ………………10分
………………10分


科目:高中数学 来源:2010年江西省高一上学期第一次月考数学卷 题型:解答题
(本题满分10分)
已知函数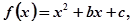 且
且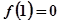 .
.
(1)若函数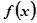 是偶函数,求函数
是偶函数,求函数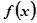 在区间
在区间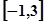 上的最大值和最小值;
上的最大值和最小值;
(2)要使函数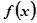 在区间
在区间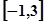 上单调递增,求
上单调递增,求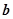 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com