Question

【题目】已知椭圆： （）的短轴长为2，以为中点的弦经过左焦点，其中点不与坐标原点重合，射线与以圆心的圆交于点.

（Ⅰ）求椭圆的方程；

（Ⅱ）若四边形是矩形，求圆的半径；

（Ⅲ）若圆的半径为2，求四边形面积的最小值.

Answer 1

【答案】(1) ;(2) .（3）四边形面积的最小值为.

【解析】试题分析：（Ⅰ）根据题意列出关于 、 、的方程组，结合性质 ， ，求出 、 、，即可得结果；（Ⅱ）设直线的方程为，直线与曲线联立，根据韦达定理结合，可求出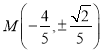，从而可得结果；（Ⅲ）根据弦长公式，点到直线距离公式和三角形面积公式可得四边形面积 ，利用单调性可得结果.

试题解析：（Ⅰ）由题意可知， ， ，则， .

所以椭圆的方程为.

（Ⅱ）由题意可知，直线不与轴垂直，且经过点，

所以可设直线的方程为.

由得.

易知判别式，设， ，则

， ①

所以，

所以的中点为.

因为四边形是矩形，所以，且.

则，即，②

又因为， ，③

由①②③解得.

所以点，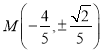

所以圆的半径.

（Ⅲ）当圆的半径为2时，由（Ⅱ）可知的中点为，

所以直线的斜率为，所以直线的方程为.

设点到直线的距离为，因为点是弦的中点，

所以点到直线的距离也为，

则.

因为点， 位于直线的异侧，所以.

所以 .

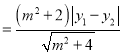又因为，

所以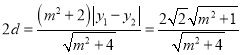

所以四边形面积

，其中.

可知当时， ，

即四边形面积的最小值为.