
分析 设f(x)=(m-1)x2+(3m+4)x+(m+1),则由题意利用二次函数的性质求得m的取值范围.
解答 解:设f(x)=(m-1)x2+(3m+4)x+(m+1),则由题意可得$\left\{\begin{array}{l}{△{=(3m+4)}^{2}-4(m-1)(m+1)≥0}\\{-1<\frac{3m+4}{2(1-m)}<1}\\{f(-1)•f(1)>0}\end{array}\right.$,
即 $\left\{\begin{array}{l}{{5m}^{2}+24m+20≥0}\\{\frac{5m+3}{2(m-1)}>0}\\{\frac{m+5}{2m-1}<0}\\{(-m-4)(5m+2)>0}\end{array}\right.$,求得-4<m≤$\frac{-12-2\sqrt{11}}{5}$.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
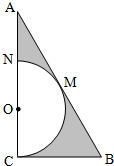 如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.
如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{6},\frac{1}{2})$ | B. | $[\frac{1}{3},\frac{1}{2}]$ | C. | $(\frac{1}{6},\frac{1}{2}]$ | D. | $[\frac{1}{3},\frac{1}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com