Question

3．如图，已知AB是半圆O的直径，O是半圆圆心，AB=8，M、N、P是将半圆圆周四等分的三个分点．
（1）从A、B、M、N、P这5个点中任取3个点，求这3个点组成等腰三角形的概率；
（2）在半圆内任取一点S，求△SOB的面积大于4$\sqrt{2}$的概率．

Answer 1

分析 （1）这是古典概型，利用列举法进行求解即可．
（2）是几何概型，求出对应区域的面积，结合几何概型的概率公式进行求解即可．

解答 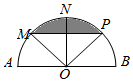解：（1）从A、B、M、N、P这5个点中任取3个点，一共可以组成10个三角形：△ABM、△ABN、△ABP、△AMN、△AMP、
△ANP、△BMN、△BMP、△BNP、△MNP，
其中是等腰三角形的只有△ABN、△ABN、△BN，△MNP，4个，
所以这3个点组成等腰三角形的概率P=$\frac{4}{10}=\frac{2}{5}$．
（2）连接MP，取线段MP的中点D，则OD⊥MP，
易求得OD=2$\sqrt{2}$，
当S点在线段MP上时，S_△ABS=$\frac{1}{2}$×2$\sqrt{2}$×4=4$\sqrt{2}$，
所以只有当S点落在阴影部分时，三角形SAB面积才能大于4$\sqrt{2}$，而
S_阴影=S_扇形OMP-S_△OMP=$\frac{1}{2}$×$\frac{π}{2}$×4²-$\frac{1}{2}$×4²=4π-8，
所以由几何概型公式得三角形SAB的面积大于4$\sqrt{2}$的概率P=$\frac{4π-8}{8π}=\frac{π-2}{2π}$．

点评 本题考查的是几何概型和古典概型的计算，利用列举法以及图象法是解决几何概型和古典概型的常用方法．