练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．求函数y=$\frac{{x}^{2}+13x+36}{x}$的最值．

    分析 对x分类讨论，利用基本不等式的性质即可得出．

    解答 解：①x＞0时，函数f（x）=y=$\frac{{x}^{2}+13x+36}{x}$=x$+\frac{36}{x}$+13≥$2\sqrt{x•\frac{36}{x}}$+13=25，当且仅当x=6时取等号，此时函数f（x）取得最小值25．
    ②x＜0时，函数y=f（x）=$\frac{{x}^{2}+13x+36}{x}$=x$+\frac{36}{x}$+13=-（-x+$\frac{36}{-x}$）+13≤-$2\sqrt{-x•\frac{36}{-x}}$+13=1，当且仅当x=-6时取等号，此时函数f（x）取得最大值1．

    点评 本题考查了基本不等式的性质，考查了分类讨论方法、推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

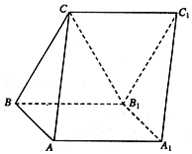    19．如图，三棱柱ABC-A1B1C1的侧面AA1B1B是边长为2的正方形，侧面BB1C1C为菱形，∠CBB1=60°，AB⊥B1C．
    （I）求证：平面AA1B1B⊥平面BB1C1C；
    （II）求三棱锥A-B1CC1体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知数列{an}，a1=1，an+1=an+2n，计算数列{an}的第100项．现已给出该问题算法的流程图（如图1所示）

    （1）请在图1中判断框的A、B、C（其中A中用i的关系表示）处填上合适的语句，使之完成该问题的算法功能．
    （2）根据流程图1补充完整程序语言（如图2）（即在D、E、F处填写合适的语句）．
    解：（将答案写在下面相应位置）

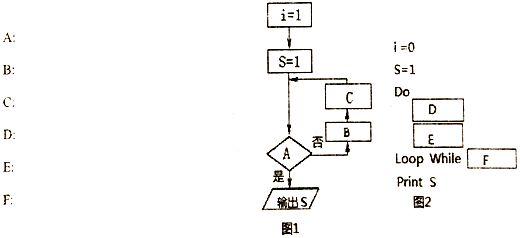
    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列函数既是偶函数又是幂函数的是（　　）
    A．y=xB．$y={x^{\frac{2}{3}}}$C．$y={x^{\frac{1}{2}}}$D．y=|x|

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知f（x）是定义在R上的奇函数，对任意x＞0，都有f（x+4）=f（x），若f（-2）=2，则f（2 018）等于（　　）
    A．2 012B．2C．2 013D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．空间直角坐标系O-xyz中，点A（3，-2，1）关于xOz坐标平面对称的点的坐标是（　　）
    A．（-3，-2，1）B．（3，2，1）C．（-3，2，-1）D．（-3，2，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．在平面直角坐标系xoy中，已知圆C1：x2+y2+6x-2y+6=0和圆C2：x2+y2-8x-10y+37=0若直线l过点A（4，0），且被圆C1截得的弦长为2$\sqrt{3}$，
    （1）求直线l的方程
    （2）求圆C2上的点到直线l的最远距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．对于定义域为R的函数f（x），若存在非零实数x0，使函数f（x）在（-∞，x0）和（x0，+∞）上与x轴均有交点，则称x0为函数f（x）的一个“界点”．则下列四个函数中，不存在“界点”的是（　　）
    A．f（x）=x2+bx-2（b∈R）B．f（x）=|x2-3|C．f（x）=1-|x-2|D．f（x）=x3+x

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．椭圆$C：{x^2}+\frac{y^2}{4}=1$的焦点坐标是（0，±$\sqrt{3}$）；长轴长为4．

    查看答案和解析>>

    同步练习册答案