【题目】下列命题中，正确的序号是_____
①直线上有两个点到平面的距离相等，则这条直线和这个平面平行；
②过球面上任意两点的大圆有且只有一个；
③直四棱柱是直平行六面体；
④
为异面直线，则过
且与
平行的平面有且仅有一个；
⑤两相邻侧面所成角相等的棱锥是正棱锥.
【答案】④
【解析】
①中直线可能与平面相交，①错误；②中若两点与圆心共线，为球的直径，大圆不唯一，②错误；由直四棱柱和直平行六面体定义可知③错误；④中，首先验证存在性，再利用反证法证明唯一性，可知④正确；⑤中通过正方形折叠可得满足题意的棱锥，但不符合正棱锥定义，知⑤错误.
①中，直线上两点若分居平面两侧，也可满足到平面距离相等，此时直线和平面相交，故①错误；
②若球面上两点构成球的直径，此时过两点的大圆不唯一，故②错误；
③若直四棱柱底面不是平行四边形，例如是梯形时，则其不是平行六面体，故③错误；
④过
上一点
作直线
，则
确定平面
且
假设存在平面
，
且
，则且，
与已知矛盾
满足题意的平面有且仅有一个，④正确；
⑤把如下图所示的正方形折叠成三棱锥，满足侧面所成角相等，此时不是正三棱锥
故⑤错误.
综上所述：正确命题的序号为④
故答案为：④
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案科目：高中数学 来源： 题型：
【题目】已知抛物线
过点
，过点
作直线
与抛物线
交于不同两点
、
，过作
轴的垂线分别与直线
、
交于点
、
，其中
为坐标原点.
（1）求抛物线的方程；
（2）写出抛物线的焦点坐标和准线方程；
（3）求证：为线段
的中点.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
.
（1）若
在区间
上不是单调函数，求实数
的范围；
（2）若对任意
，都有
恒成立，求实数
的取值范围；
（3）当
时，设
，对任意给定的正实数，曲线
上是否存在两点
，
，使得
是以
（为坐标原点）为直角顶点的直角三角形，而且此三角形斜边中点在
轴上？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】学校艺术节对同一类的
，
，
，
四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：
甲说：“是或作品获得一等奖”；
乙说：“作品获得一等奖”；
丙说：“，两项作品未获得一等奖”；
丁说：“是作品获得一等奖”.
若这四位同学中只有两位说的话是对的，则获得一等奖的作品是__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示：在五面体ABCDEF中，四边形EDCF是正方形，AD＝DE＝1，∠ADE＝90°，∠ADC＝∠DCB＝120°．
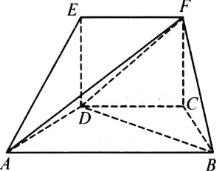
（Ⅰ）求证：平面ABCD⊥平面EDCF；
（Ⅱ）求三棱锥A－BDF的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系中已知A(4,O)、B(0,2)、C(-1,0)、D(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
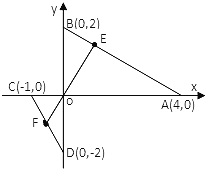
(1)若F为线段CD的中点,证明:
；
(2)“若F为线段CD的中点,则”的逆命题是否成立?说明理由；
(3)设
,求
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
