
【题目】随着经济的发展和个人收入的提高,自2018年10月1日起,个人所得税起征点和税率依法进行调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率( | 级数 | 全月应纳税所得额 | 税率( |
1 | 不超过1500元的部分 | 3 | 1 | 不超过3000元的部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
… | … | … | … | … | … |
(1)假如小李某月的工资、薪金等所得税前收入为7500元时,请你帮小李算一下调整后小李的实际收入比调整前增加了多少?
(2)某税务部门在小李所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入 (元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用
的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,
元的人数,![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,随机变量
元的人数,随机变量![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)220元;(2)见解析
【解析】
(1)根据税率表直接算出之后作比较即可
(2)由频数分布表可知从![]() 及
及![]() 的人群中抽取7人,其中
的人群中抽取7人,其中![]() 中占3人,
中占3人,![]() 的人中占4人,再从这7人中选4人,所以
的人中占4人,再从这7人中选4人,所以![]() 的取值可能为0,2,4,然后分别算出每种情况的概率即可.
的取值可能为0,2,4,然后分别算出每种情况的概率即可.
(1)由于小李的工资、薪金等收入为7500元,
按调整前起征点应纳个税为![]() 元;
元;
按调整后起征点应纳个税为![]() 元,
元,
比较两个纳税方案可知,按调整后起征点应纳个税少交220元,
即个人的实际收入增加了220元,所以小李的实际收入增加了220元.
(2)①由频数分布表可知从![]() 及
及![]() 的人群中抽取7人,
的人群中抽取7人,
其中![]() 中占3人,
中占3人,![]() 的人中占4人,
的人中占4人,
再从这7人中选4人,所以![]() 的取值可能为0,2,4,
的取值可能为0,2,4,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
所以其分布列为
| 0 | 2 | 4 |
|
|
|
|
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1970年4月24日,我国发射了自己的第一颗人造地球卫星“东方红一号”,从此我国开启了人造卫星的新篇章,人造地球卫星绕地球运行遵循开普勒行星运动定律:卫星在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为![]() ,
,![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
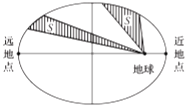
A.卫星向径的最小值为![]()
B.卫星向径的最大值为![]()
C.卫星向径的最小值与最大值的比值越小,椭圆轨道越扁
D.卫星运行速度在近地点时最小,在远地点时最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生营养餐由A和B两家配餐公司配送. 学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分. 根据收集的80份问卷的评分,得到A公司满意度评分的频率分布直方图和B公司满意度评分的频数分布表:

(Ⅰ)根据A公司的频率分布直方图,估计该公司满意度评分的中位数;
(Ⅱ)从满意度高于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率;
(Ⅲ)请从统计角度,对A、B两家公司做出评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型水库的管理部门为研究库区水量的变化情况,决定安排两个小组在同一年中各自独立的进行观察研究.其中一个小组研究水源涵养情况.他们通过观察入库的若干小溪和降雨量等因素,随机记录了![]() 天的日入库水量数据(单位:千
天的日入库水量数据(单位:千![]() ),得到下面的柱状图(如图甲).另一小组则研究由于放水、蒸发或渗漏造成的水量消失情况.他们通过观察与水库相连的特殊小池塘的水面下降情况来研究库区水的整体消失量,随机记录了
),得到下面的柱状图(如图甲).另一小组则研究由于放水、蒸发或渗漏造成的水量消失情况.他们通过观察与水库相连的特殊小池塘的水面下降情况来研究库区水的整体消失量,随机记录了![]() 天的库区日消失水量数据(单位:千
天的库区日消失水量数据(单位:千![]() ),并将观测数据整理成频率分布直方图(如图乙).
),并将观测数据整理成频率分布直方图(如图乙).
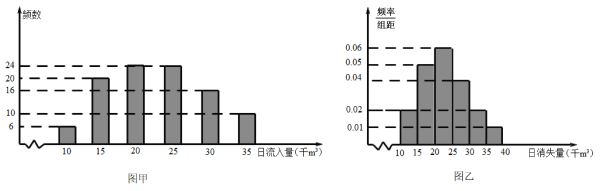
(1)据此估计这一年中日消失水量的平均值;
(2)以频率作为概率,试解决如下问题:
①分别估计日流入水量不少于![]() 千
千![]() 和日消失量不多于
和日消失量不多于![]() 千
千![]() 的概率;
的概率;
②试估计经过一年后,该水库的水量是增加了还是减少了,变化的量是多少?(一年按![]() 天计算),说明理由.
天计算),说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《增删算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关.”则下列说法正确的是( )
A.此人第二天走了九十六里路B.此人第三天走的路程站全程的![]()
C.此人第一天走的路程比后五天走的路程多六里D.此人后三天共走了42里路
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,点E在AB上,AE=2EB=2,且DE⊥AB.以DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.
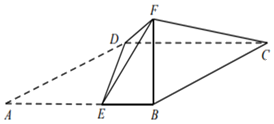
(1)求证:平面BFC⊥平面BCDE;
(2)若直线DF与平面BCDE所成角的正切值为![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com