【题目】若函数
， 
， 
， 
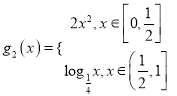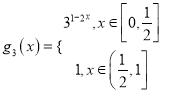在等差数列
中, 
，
用
表示数列
的前2018项的和，则（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】等差数列{an}中,a1=0,a2019=1,可知该数列为递增数列,且a1010=
,a505<
,a506>
，
对于g1(x)=2x,该函数在[0,1]上单调递增,于是有g1(an+1)g1(an)>0，
于是bn=g1(an+1)g1(an)，
∴P1=g1(a2019)g1(a1)=21=1，
对于g2(x),该函数在
上递增，在区间
上单调递减，
于是P2=g2(a1010)g2(a1)+g2(a1010)g2(a2019)= 
，对于g3(x),该函数在
上单调递减，在区间
上是常函数，
于是P3=g3(a1010)+g3(a1) =
，
对于g4(x),该函数在
和
递增,在
和
上递减,且是以
为周期的周期函数，故只需讨论
的情况，再2倍即可.仿前可知：
P4=2[g4(a505)g4(a1)+g4(a506)g4(a1010)]
<
，故P4<1，
综上可得： 
.
本题择A选项.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】设a，b∈R，函数 
，g（x）=ex（e为自然对数的底数），且函数f（x）的图象与函数g（x）的图象在x=0处有公共的切线．
（Ⅰ）求b的值；
（Ⅱ）讨论函数f（x）的单调性；
（Ⅲ）若g（x）＞f（x）在区间（﹣∞，0）内恒成立，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我国加入WTO时，根据达成的协议，某产品的市场供应量P与市场价格x的关系近似满足P(x)＝2(1－kt)(x－b)2(其中t为关锐的税率，且t∈[0， 
)，x为市场价格，b、k为正常数)．当t＝
时的市场供应量曲线如图所示．
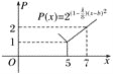
(1)根据图象求b、k的值；
(2)记市场需求量为Q，它近似满足Q(x)＝
，当P＝Q时的市场价格称为市场平衡价格，为使市场平衡价格不低于9元，求税率的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设y=f(t)是某港口水的深度y(米)关于时间t(小时)的函数，其中
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 12 | 15.1 | 12.1 | 9.1 | 12 | 14.9 | 11.9 | 9 | 12.1 |
经长期观察，函数y=f(t)的图象可以近似地看成函数
的图象.⑴求
的解析式；⑵设水深不小于
米时，轮船才能进出港口。某轮船在一昼夜内要进港口靠岸办事，然后再出港。问该轮船最多能在港口停靠多长时间？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，AD∥BC，CD=13，AB=12，BC=10，AD=5，PD=8，点E，F分别是PB，DC的中点．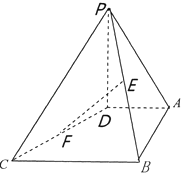
（1）求证：EF∥平面PAD；
（2）求EF与平面PDB所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ax3+3x2+1，若至少存在两个实数m，使得f（﹣m），f（1）、f（m+2）成等差数列，则过坐标原点作曲线y=f（x）的切线可以作（ ）
A.3条
B.2条
C.1条
D.0条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
