
����Ŀ��Ϊ���о����ýγ��ڸ��ٹ�·�ϵij����������ͨ���������50�����ýγ���ʻԱ���е��飬�õ����ڸ��ٹ�·����ʻʱ��ƽ���������Ϊ����30�����Լ�ʻԱ�У�ƽ�����ٳ���![]() ����20�ˣ�������
����20�ˣ�������![]() ����10�ˣ���20��Ů�Լ�ʻԱ�У�ƽ�����ٳ���
����10�ˣ���20��Ů�Լ�ʻԱ�У�ƽ�����ٳ���![]() ����5�ˣ�������
����5�ˣ�������![]() ����15�ˣ�
����15�ˣ�
�����������������������ж��Ƿ���99.5%�İ�����Ϊƽ�����ٳ���![]() �������Ա��йأ�
�������Ա��йأ�
ƽ�����ٳ���
| ƽ�����ٲ�����
| �ϼ� | |
���Լ�ʻԱ���� | |||
Ů�Լ�ʻԱ���� | |||
�ϼ� |
���� �������������������������壬�ִӸ��ٹ�·����ʻ�Ĵ������ýγ��������ȡ3��������3�����м�ʻԱΪŮ���ҳ��ٲ�����![]() �ij�����Ϊ
�ij�����Ϊ![]() ����ÿ�γ�ȡ�Ľ����������ģ���
����ÿ�γ�ȡ�Ľ����������ģ���![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�ο���ʽ�� ![]() ������
������![]() ��
��
�ο����ݣ�
| 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡�������![]() �İ��գ�����
�İ��գ����� ![]() ���ֲ��м�����
���ֲ��м�����
���������������: �����ȸ���������д����ע���Ӧ��ϵ�����ٴ��빫ʽ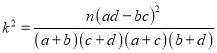 ��������������ο����ݽ��ж��գ�ȷ�������ʷ�Χ�������ж��Ƿ���
��������������ο����ݽ��ж��գ�ȷ�������ʷ�Χ�������ж��Ƿ���![]() �İ���.������Ƶ�ʹ��Ƹ��ʵã���ʻԱΪŮ���ҳ��ٲ�����
�İ���.������Ƶ�ʹ��Ƹ��ʵã���ʻԱΪŮ���ҳ��ٲ�����![]() �ij����ĸ���Ϊ
�ij����ĸ���Ϊ![]() .��������������Ӷ���ֲ�
.��������������Ӷ���ֲ�![]() �����ݹ�ʽ
�����ݹ�ʽ![]() �ɵ����������Ӧ�ĸ��ʣ��б��ɵ÷ֲ��У�����
�ɵ����������Ӧ�ĸ��ʣ��б��ɵ÷ֲ��У�����![]() �ɵ���ѧ����.
�ɵ���ѧ����.
�������:�⣺����
ƽ���������� ���� | ƽ�����ٲ����� ���� | �ϼ� | |
���Լ�ʻԱ���� | 20 | 10 | 30 |
Ů�Լ�ʻԱ���� | 5 | 15 | 20 |
�ϼ� | 25 | 25 | 50 |
![]() ��
��
![]() ������
������![]() �İ�����Ϊƽ�����ٳ���
�İ�����Ϊƽ�����ٳ���![]() ���Ա��й�.
���Ա��й�.
�������������������˼�룬�Ӹ��ٹ�·����ʻ�Ĵ������ýγ����漴��ȡ1������ʻԱΪŮ���ҳ��ٲ�����![]() �ij����ĸ���Ϊ
�ij����ĸ���Ϊ![]() .
.
![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ����
����![]() ��
��
![]() ��
��
![]() ��
��
�ֲ���Ϊ��
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2��2mx��4m2��6��0�������ȸ�Ϊ�����£�����(����1)2��(�£�1)2����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)��a��![]() .
.
(1)��f(0)��
(2)̽��f(x)�ĵ����ԣ���֤����Ľ��ۣ�
(3)��f(x)Ϊ�溯����������f(ax)<f(2)��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC�ļ����귽��Ϊ![]() ��ֱ��
��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ����ֱ��
����ֱ��![]() ��ԲC�ཻ�ڲ�ͬ������P��Q��
��ԲC�ཻ�ڲ�ͬ������P��Q��
����д��ԲC��ֱ�����귽�̣�����Բ�ĵ�������뾶��
�������ҳ�|PQ|=4����ֱ��![]() ��б�ʣ�
��б�ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ����������ֱ�Ϊ
����������ֱ�Ϊ![]() ��������Ϊ
��������Ϊ![]() .�����
.�����![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �ཻ�ڲ�ͬ����
�ཻ�ڲ�ͬ����![]() ��
�� ![]() �ܳ�Ϊ
�ܳ�Ϊ![]() .
.
����������ԲC�ı����̣�
������֪��![]() ��֤������ֱ��
��֤������ֱ��![]() �仯ʱ������TA��
�仯ʱ������TA��![]() ��б��֮��Ϊ��ֵ��
��б��֮��Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() �DZ߳�Ϊ2�������Σ�
�DZ߳�Ϊ2�������Σ�![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬ƽ��
���е㣬ƽ��![]() ƽ��
ƽ��![]() ����
����![]() .
.
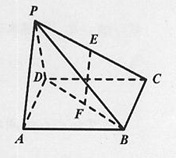
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=![]() +x��x=1�������߷���Ϊ2x��y+b=0��
+x��x=1�������߷���Ϊ2x��y+b=0��
������ʵ��a��b��ֵ��
����������g��x��=f��x��+![]() x2��kx����g��x�����䶨�����ϵ�����������ʵ��k��ȡֵ��Χ��
x2��kx����g��x�����䶨�����ϵ�����������ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A�����ұ��������ʵĺ���![]() ��ɵģ�
��ɵģ�
�ٺ���![]() �Ķ�������
�Ķ�������![]() ���ں���
���ں���![]() ��ֵ����
��ֵ����![]() ��
��
�ۺ���![]() ��
��![]() �������������Էֱ�̽��������С�⣺
�������������Էֱ�̽��������С�⣺
��1���жϺ�����![]() ��
��![]() �Ƿ����ڼ���A������Ҫ˵�����ɣ�
�Ƿ����ڼ���A������Ҫ˵�����ɣ�
��2�����ڣ�1��������Ϊ���ڼ���A�ĺ���![]() ������ʽ
������ʽ![]()
�Ƿ���������![]() ��������������������֤����������������˵�����ɡ�
��������������������֤����������������˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
�� ![]() ���Һ���
���Һ���![]() ��ͼ�����ֱ��
��ͼ�����ֱ��![]() �Գơ�
�Գơ�
(1)����![]() ������
������![]() �����ֵ��
�����ֵ��
(2)��![]() ������ʽ
������ʽ![]() ��
��![]() �Ϻ��������ʵ��
�Ϻ��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(3)��![]() ��Ψһ��㣬��ʵ��
��Ψһ��㣬��ʵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com