
【题目】从8名运动员中选4人参加![]() 米接力赛,在下列条件下,各有多少种不同的排法?
米接力赛,在下列条件下,各有多少种不同的排法?
(1)甲、乙两人必须入选且跑中间两棒;
(2)若甲、乙两人只有一人被选且不能跑中间两棒;
(3)若甲、乙两人都被选且必须跑相邻两棒;
(4)甲不在第一棒.
【答案】(1)60;(2)480;(3)180;(4)1470
【解析】
(1)先![]() 选好参赛选手,再
选好参赛选手,再![]() 安排好甲、乙两人,再
安排好甲、乙两人,再![]() 安排剩余两人,相乘得到结果;(2)先确定参赛选手,共有
安排剩余两人,相乘得到结果;(2)先确定参赛选手,共有![]() 种选法;再
种选法;再![]() 安排好甲或乙,继续
安排好甲或乙,继续![]() 安排好剩余三人,相乘得到结果;(3)先
安排好剩余三人,相乘得到结果;(3)先![]() 选好参赛选手,再用捆绑法求得结果;(4)先
选好参赛选手,再用捆绑法求得结果;(4)先![]() 安排好第一棒,再
安排好第一棒,再![]() 安排好其余三棒,相乘得到结果.
安排好其余三棒,相乘得到结果.
(1)除甲、乙外还需选择![]() 人参加接力赛共有
人参加接力赛共有![]() 种选法
种选法
则甲、乙跑中间两棒共有![]() 种排法;另外
种排法;另外![]() 人跑另外两棒共有
人跑另外两棒共有![]() 种排法
种排法
![]() 甲、乙两人必须入选且跑中间两棒共有:
甲、乙两人必须入选且跑中间两棒共有:![]() 种排法
种排法
(2)甲、乙只有一人入选且选另外选![]() 人参加接力赛共有
人参加接力赛共有![]() 种选法
种选法
甲或乙不跑中间两棒共有![]() 种排法;其余
种排法;其余![]() 人跑剩余三棒共有
人跑剩余三棒共有![]() 种排法
种排法
![]() 甲、乙两人只有一人被选且不能跑中间两棒共有:
甲、乙两人只有一人被选且不能跑中间两棒共有:![]() 种排法
种排法
(3)除甲、乙外还需选择![]() 人参加接力赛共有
人参加接力赛共有![]() 种选法
种选法
甲乙跑相邻两棒,其余![]() 人跑剩余两棒共有
人跑剩余两棒共有![]() 种排法
种排法
![]() 甲、乙两人都被选且必须跑相邻两棒共有:
甲、乙两人都被选且必须跑相邻两棒共有:![]() 种排法
种排法
(4)甲不在第一棒则需选择一人跑第一棒,共有![]() 种选法
种选法
其余三棒共有![]() 种排法
种排法
![]() 甲不在第一棒共有
甲不在第一棒共有![]() 种排法
种排法


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】根据以往的经验,某建筑工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:

根据某气象站的资料,某调查小组抄录了该工程施工地某月前20天的降水量的数据,绘制得到降水量的折线图,如下图所示.
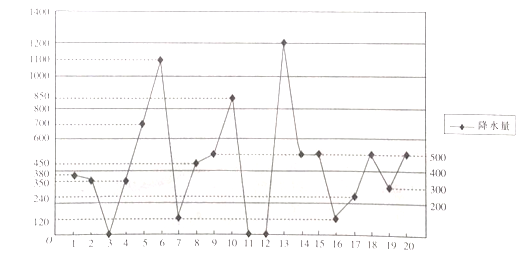
(1)求这20天的平均降水量;
(2)根据降水量的折线图,分别估计该工程施工延误天数![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() (
(![]() ,
,![]() )具有性质P;对任意的i,j(
)具有性质P;对任意的i,j(![]() ),
),![]() 与
与![]() 两数中至少有一个属于A.
两数中至少有一个属于A.
(1)分别判断数集![]() 与
与![]() 是否具有性质P,并说明理由;
是否具有性质P,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)当![]() 时,若
时,若![]() ,求集合A.
,求集合A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三有500名学生,在一次考试的英语成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
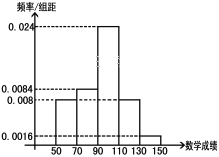
(Ⅰ)如果成绩大于135的为特别优秀,则本次考试英语、数学特别优秀的大约各多少人?
(Ⅱ)试问本次考试英语和数学的成绩哪个较高,并说明理由.
(Ⅲ)如果英语和数学两科都特别优秀的共有6人,从(Ⅰ)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望。
的分布列和数学期望。
参考公式及数据:
若![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国青年报》2015年5月14日报道:“伴随着网络技术的蓬勃发展,国内电子商务获得了爆炸式的增长,2014年网上零售额达到了27898亿元,占社会消费品零售总额的10%,也就是说,人们日常消费中10%是通过网购,而且还以年30%,40%的速度增长."假设2014-2020年网上零售额每年的增长率均为35%,试算出2015-2020年每年的网上零售额(精确到1亿元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 为曲线
为曲线![]() 上的动点,
上的动点,![]() 与
与![]() 轴、
轴、![]() 轴的正半轴分别交于
轴的正半轴分别交于![]() ,
,![]() 两点.
两点.
(1)求线段![]() 中点
中点![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)若![]() 是(1)中点
是(1)中点![]() 的轨迹上的动点,求
的轨迹上的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产![]() 、
、![]() 两种产品,生产每
两种产品,生产每![]() 产品所需的劳动力和煤、电消耗如下表:
产品所需的劳动力和煤、电消耗如下表:
产品品种 | 劳动力(个) | 煤 | 电 |
|
|
|
|
|
|
|
|
已知生产![]() 产品的利润是
产品的利润是![]() 万元,生产
万元,生产![]() 产品的利润是
产品的利润是![]() 万元.现因条件限制,企业仅有劳动力
万元.现因条件限制,企业仅有劳动力![]() 个,煤
个,煤![]() ,并且供电局只能供电
,并且供电局只能供电![]() ,则企业生产
,则企业生产![]() 、
、![]() 两种产品各多少吨,才能获得最大利润?
两种产品各多少吨,才能获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com